∇-Prox: Differentiable Proximal Algorithm Modeling for Large-Scale Optimization
SIGGRAPH 2023
∇-Prox is a domain-specific language (DSL) and compiler that transforms optimization problems into differentiable proximal solvers. Departing from handwriting these solvers and differentiating via autograd, ∇-Prox requires only a few lines of code to define a solver that can be specialized to respect a memory or training budget by optimized algorithm unrolling, deep equilibrium learning, and deep reinforcement learning. ∇-Prox allows for rapid prototyping of learning-based bi-level optimization problems for a diverse range of applications. We compare our framework against existing methods with naive implementations. ∇-Prox programs requirer fewer lines of code and compare favorably in memory consumption for diverse tasks.
Paper
Zeqiang Lai, Kaixuan Wei, Ying Fu, Philipp Härtel, Felix Heide
∇-Prox: Differentiable Proximal Algorithm Modeling for Large-Scale Optimization
SIGGRAPH 2023
Abstract
Tasks across diverse application domains can be posed as large-scale optimization problems. These include graphics, vision, machine learning, imaging, health, scheduling, planning, and energy system forecasting. Independently of the application domain, proximal algorithms have emerged as a formal optimization method that successfully solves a wide array of existing problems, often exploiting problem-specific structures in the optimization. Although model-based formal optimization provides a principled approach to problem modeling with convergence guarantees, at first glance, this seems to be at odds with black-box deep learning methods. A recent line of work shows that model-based optimization methods are effective and interpretable when combined with learning-based ingredients, allowing for generalization to a broad spectrum of applications with little or no extra training data. However, experimenting with such hybrid approaches for different tasks by hand requires domain expertise in both proximal optimization and deep learning, which is often error-prone and time-consuming. Moreover, naively unrolling these iterative methods produces lengthy compute graphs, which, when differentiated via autograd techniques, results in exploding memory consumption, making batch-based training challenging. In this work, we introduce ∇-Prox, a domain-specific modeling language and compiler for large-scale optimization problems using differentiable proximal algorithms. ∇-Prox allows users to specify optimization objective functions of unknowns concisely at a high level, and intelligently compiles the problem into compute and memory-efficient differentiable solvers. One of the core features of ∇-Prox is its full differentiability, which supports hybrid model- and learning-based solvers integrating proximal optimization with neural network pipelines. Example applications of this methodology include learning-based priors and/or sample-dependent inner-loop optimization schedulers, learned with deep equilibrium learning or deep reinforcement learning. With a few lines of code, we show ∇-Prox can generate performant solvers for a range of image optimization problems, including end-to-end computational optics, image deraining, and compressive magnetic resonance imaging. We also demonstrate ∇-Prox can be used in a completely orthogonal application domain of integrated energy system planning, an essential task in the energy crisis and the clean energy transition, where it outperforms state-of-the-art CVXPY and commercial Gurobi solvers.
Formulating Proximal Optimization in ∇-Prox
∇-Prox provides a high-level abstraction that allows for intutive conversion between mathematical and programming representations. Conversion begins by formulating problems as general optimization problems with a sum of penalties and a list of constraints, and then cast them into programs using our domain-specific modeling language.
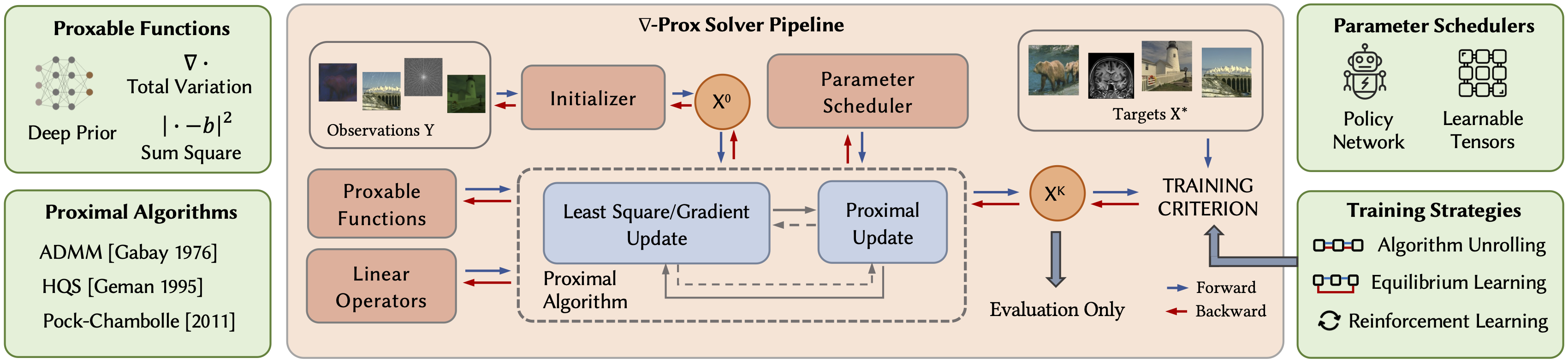
∇-Prox Solver Pipeline
∇-Prox takes a user problem description and solver choice as inputs and then automatically compiles them into an efficient differentiable solver that can be combined with other differentiable algorithm components. It supports hybrid model-based and learning-based solvers blending proximal optimization with neural network pipelines. Users can train hybrid solvers with distinct learning strategies, including algorithm unrolling, deep equilibrium learning, and deep reinforcement learning. As such, ∇-Prox allows for rapid experimentation with a variety of learned solvers and training approaches without the pain of manually implementing these methods and training schemes.
End-to-End Computational Optics
∇-Prox example tackling end-to-end computational thin-lens imaging that jointly optimizes a diffractive optical element (DOE) with an image reconstruction algorithm. The problem of co-designing the DOE and a proximal image reconstruction can be expressed in a few lines of code.
x = Variable() psf = build_doe_model().psf data_term = sum_squares(conv(x, psf) - y) reg_term = deep_prior(x, 'ffdnet', trainable=True) out = compile(data_term + reg_term, method='admm').solve()
Compressive Magnetic Resonance Imaging
Recovering high-quality images from undersampled MRI data is an ill-posed inverse imaging problem with a forward model that can be mathematically expressed as a partially sampled Fourier transform. With this forward model in hand, ∇-Prox allows users to employ ADMM with learned plug-and-play (PnP) denoising prior with a few lines of code.
x = Variable() objective = csmri(x, b) + deep_prior(x, 'unet') prob = Problem( objective ) output = prob.solve(method='admm')
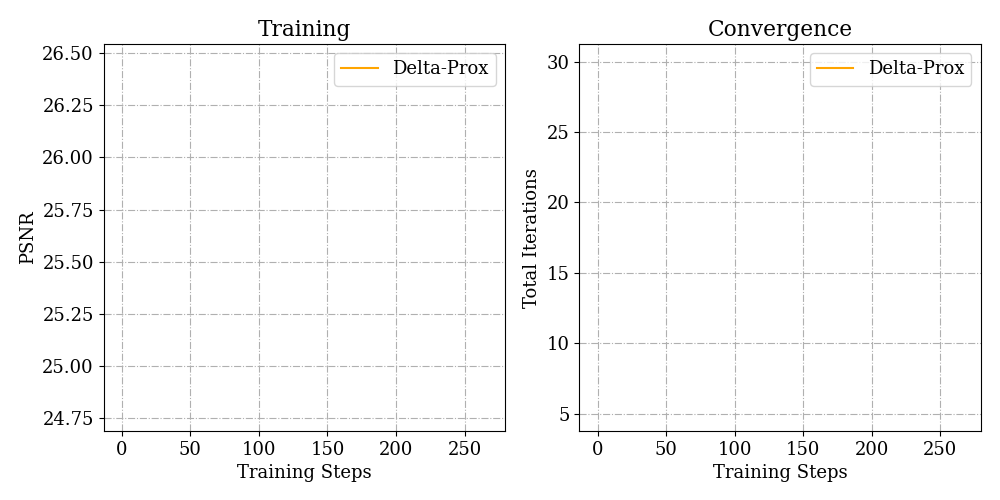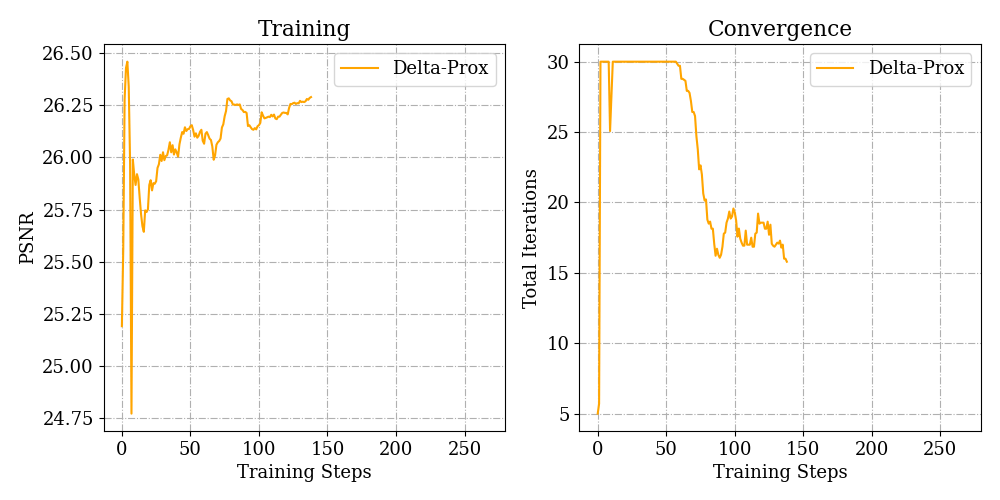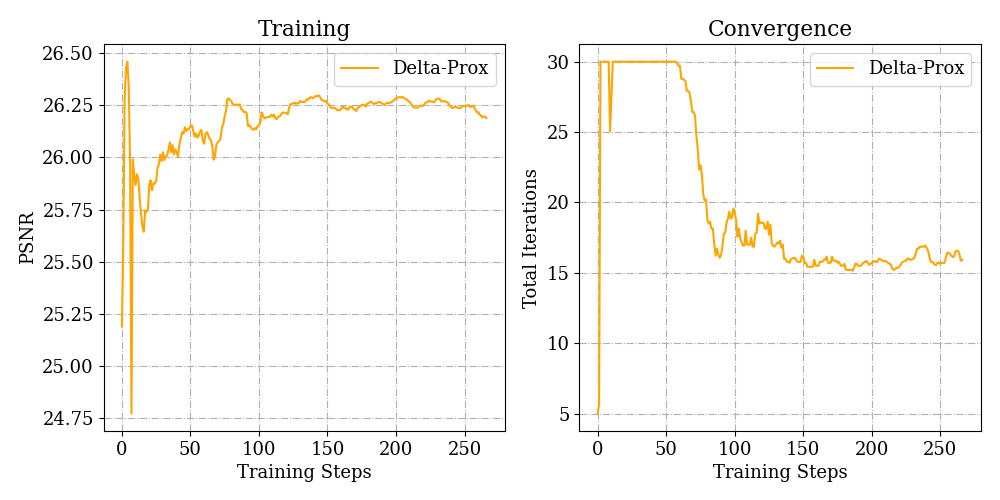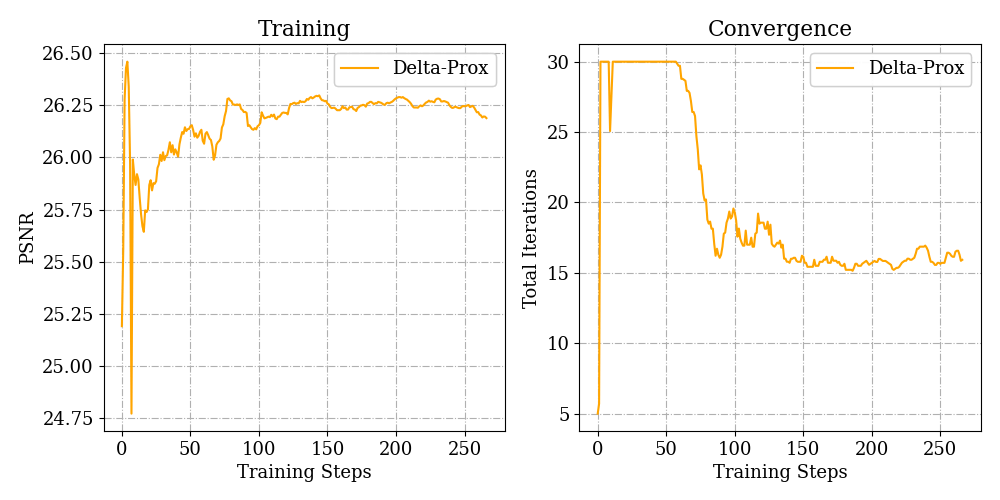
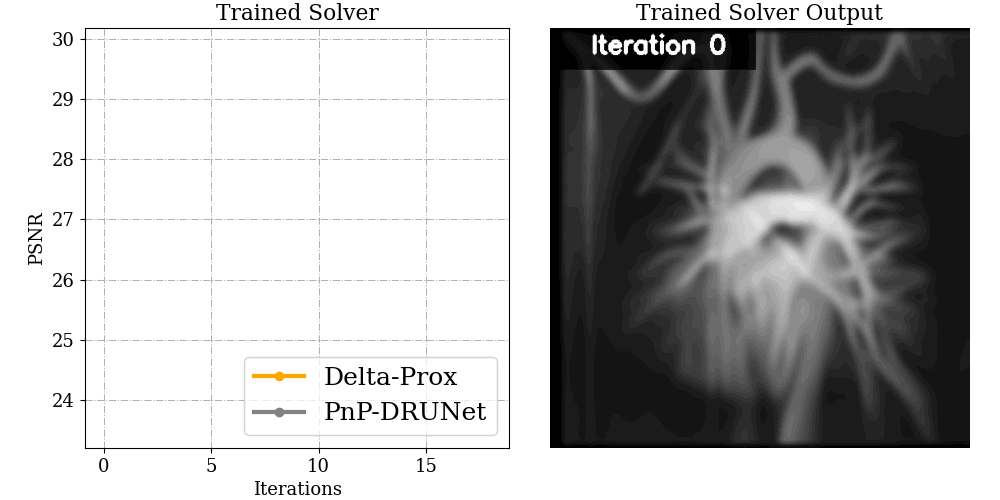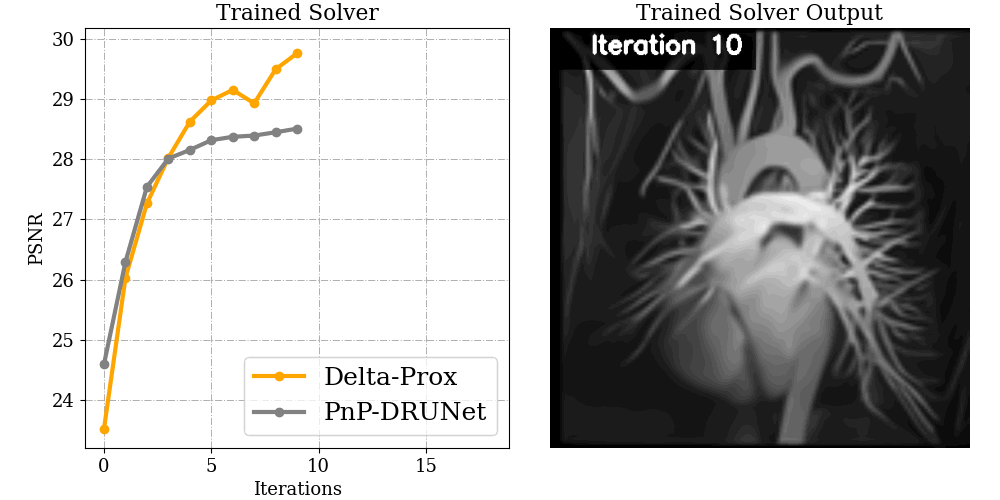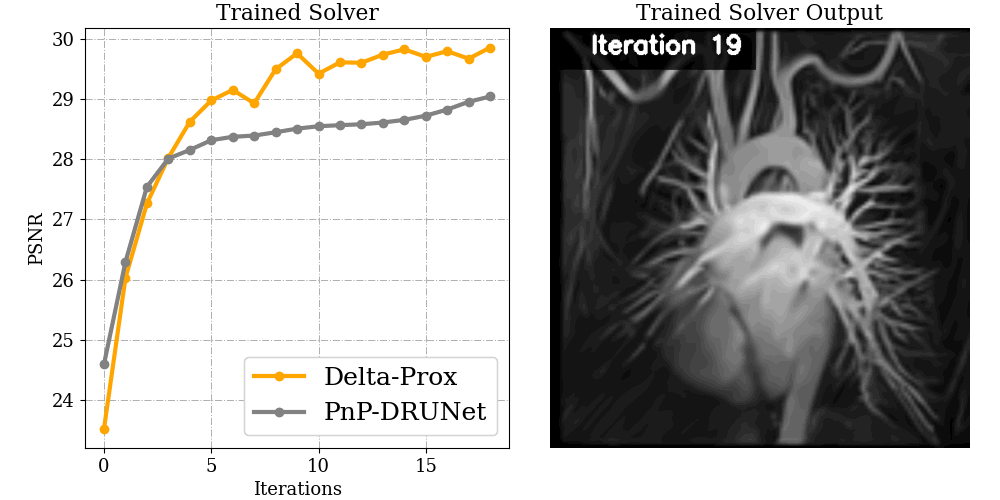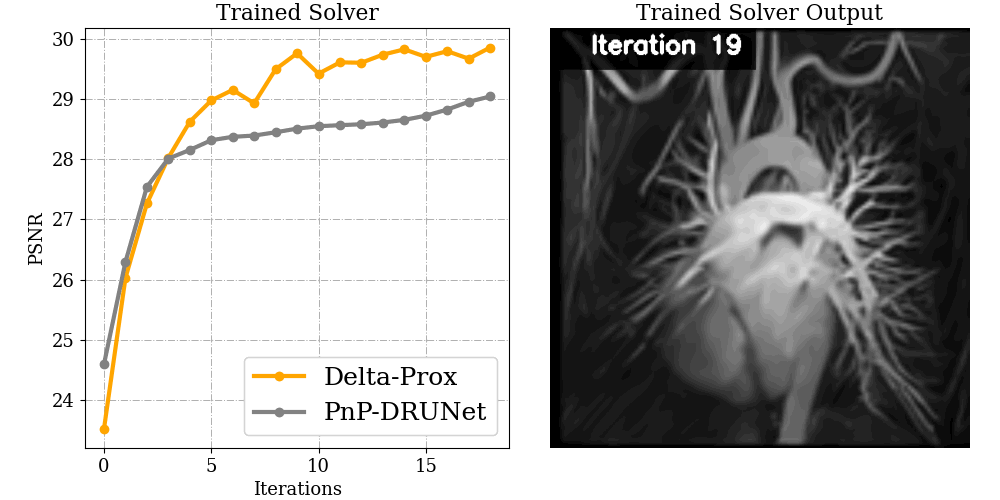
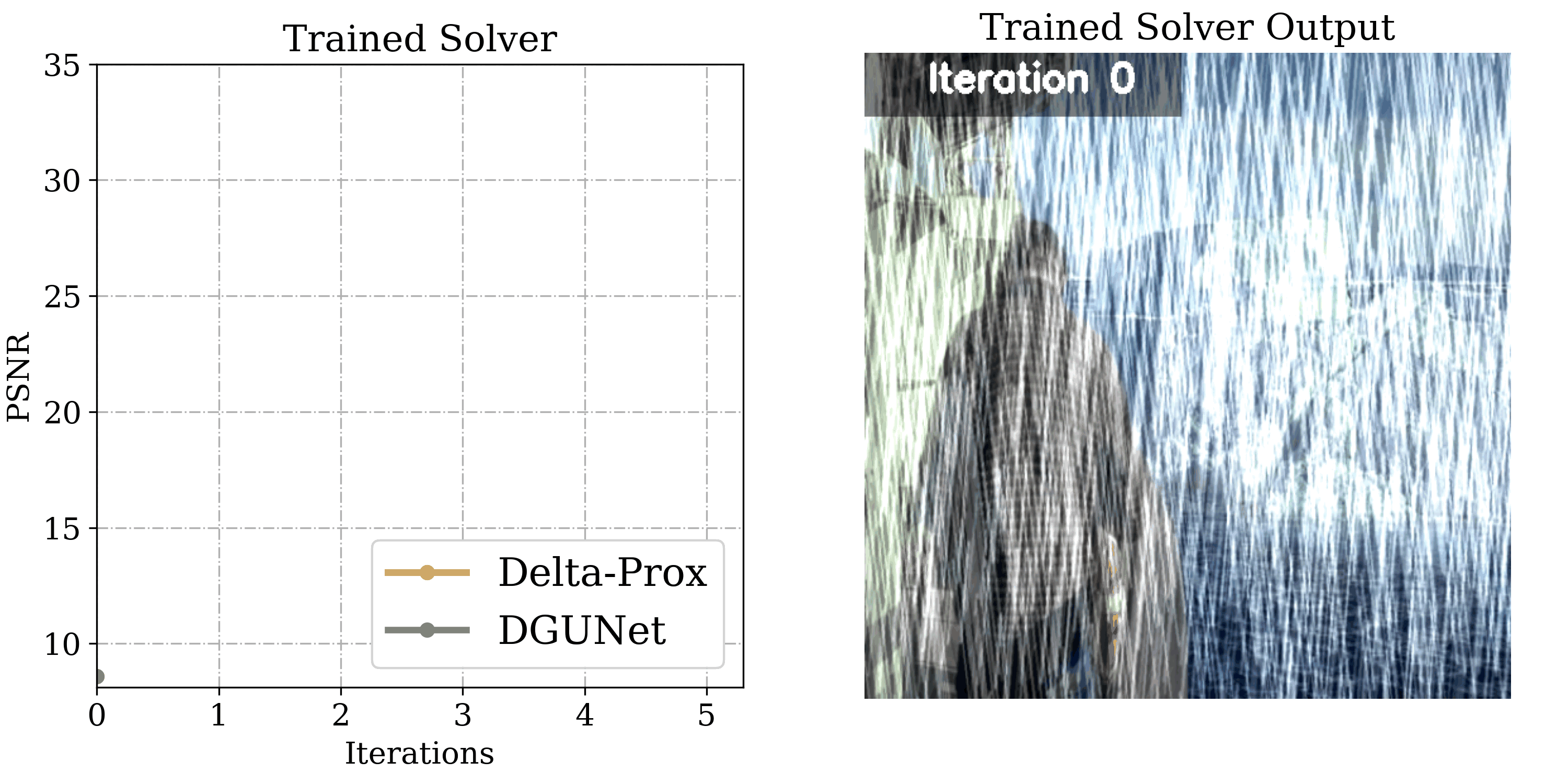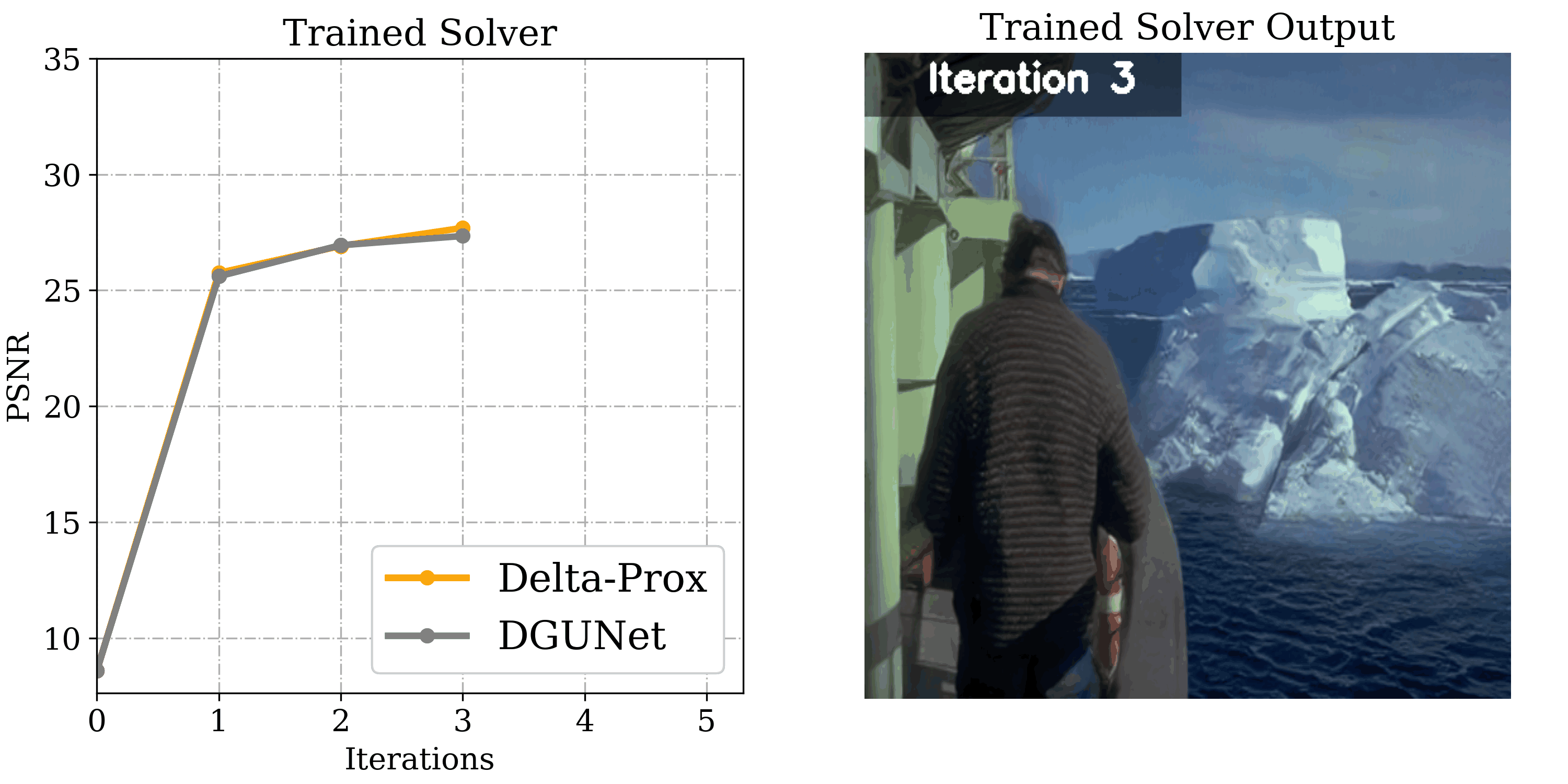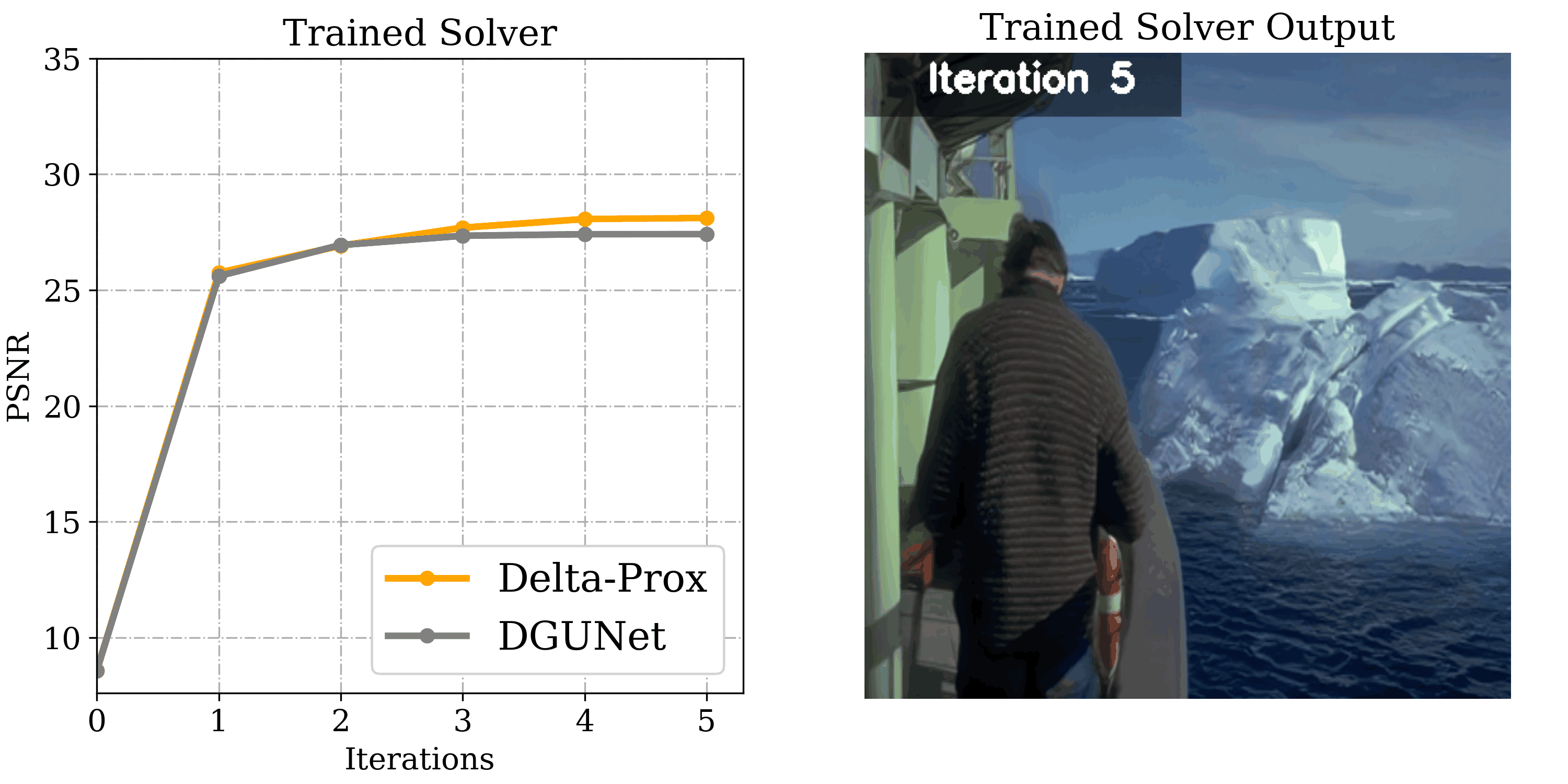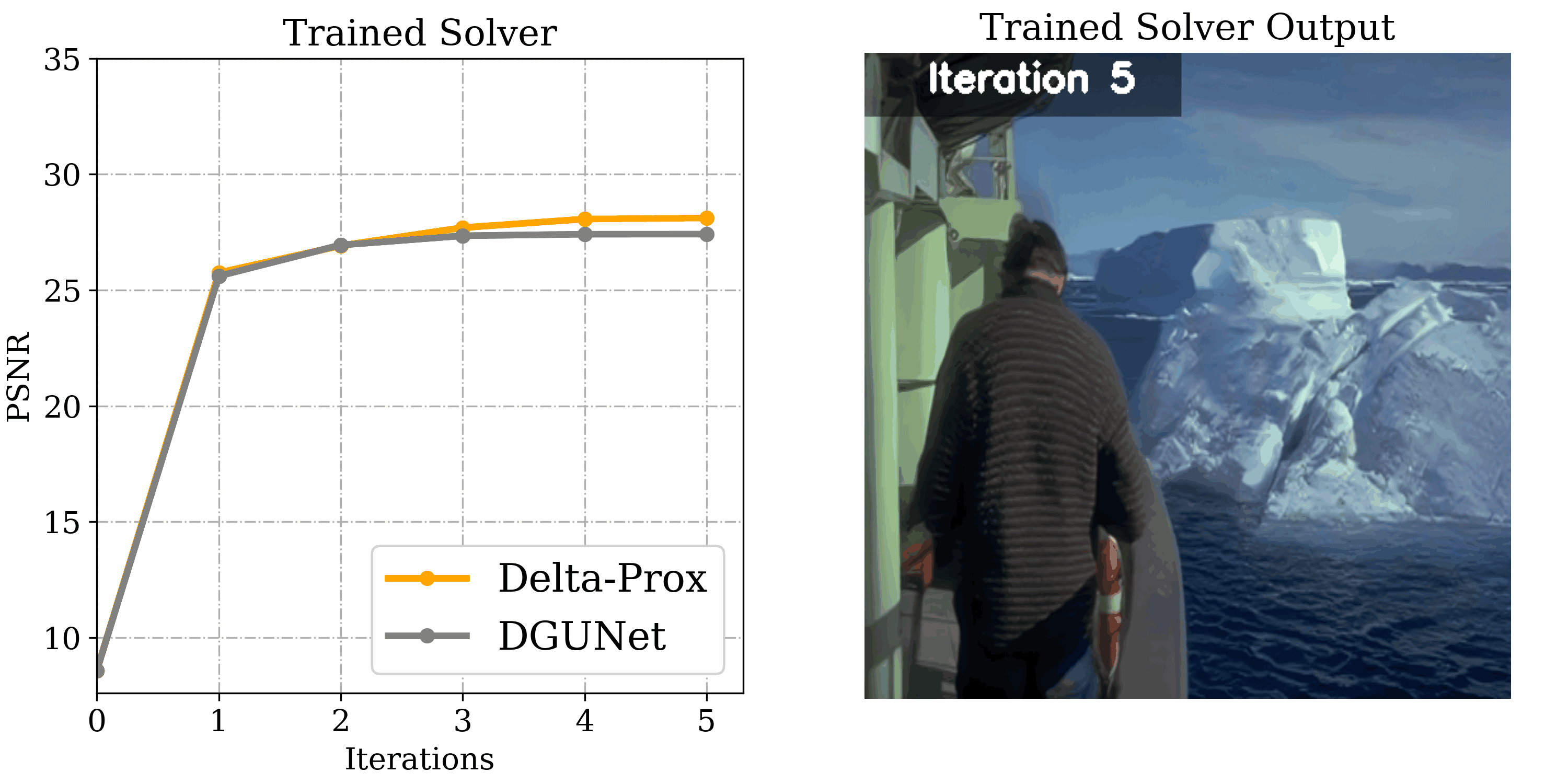
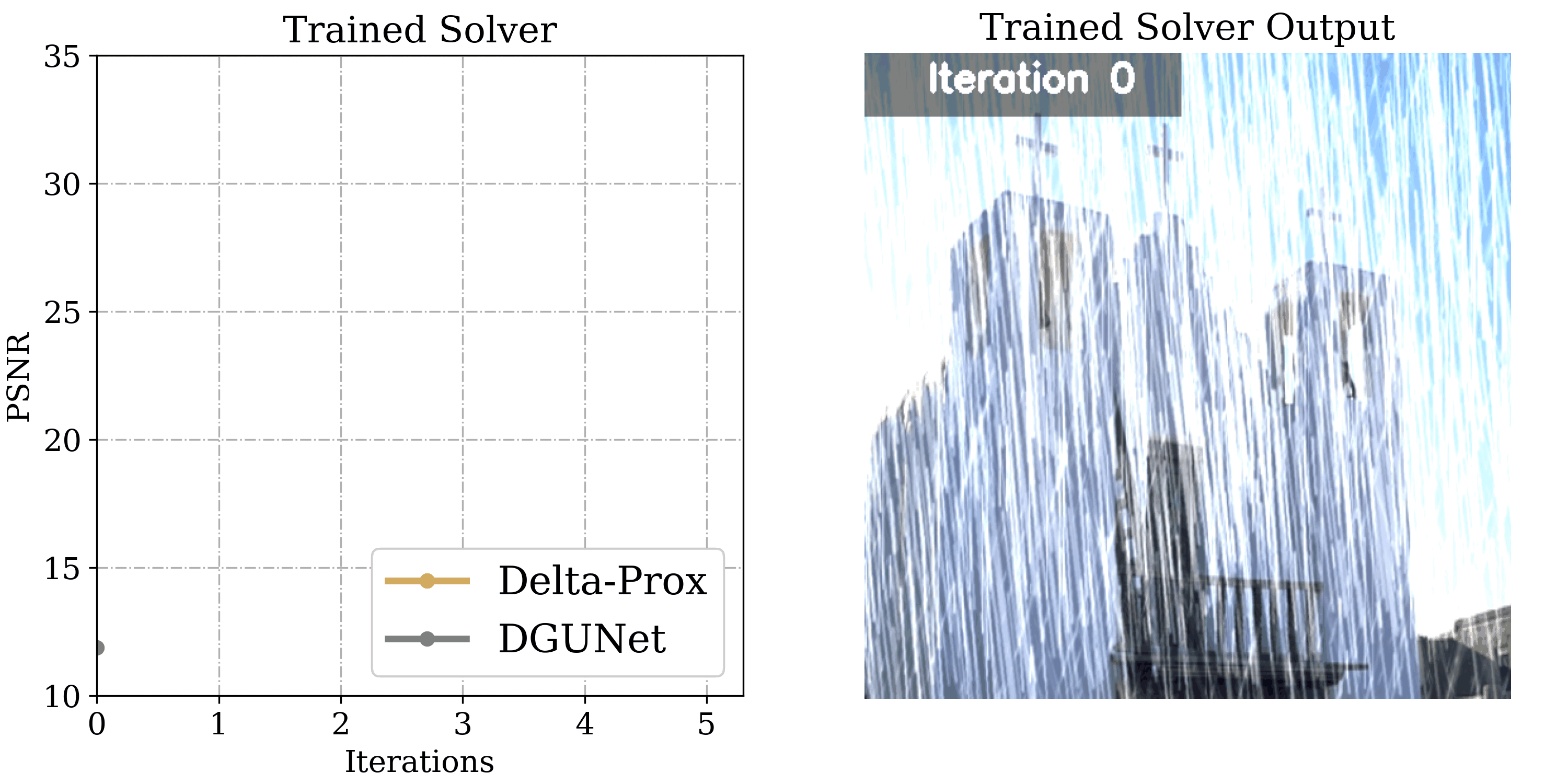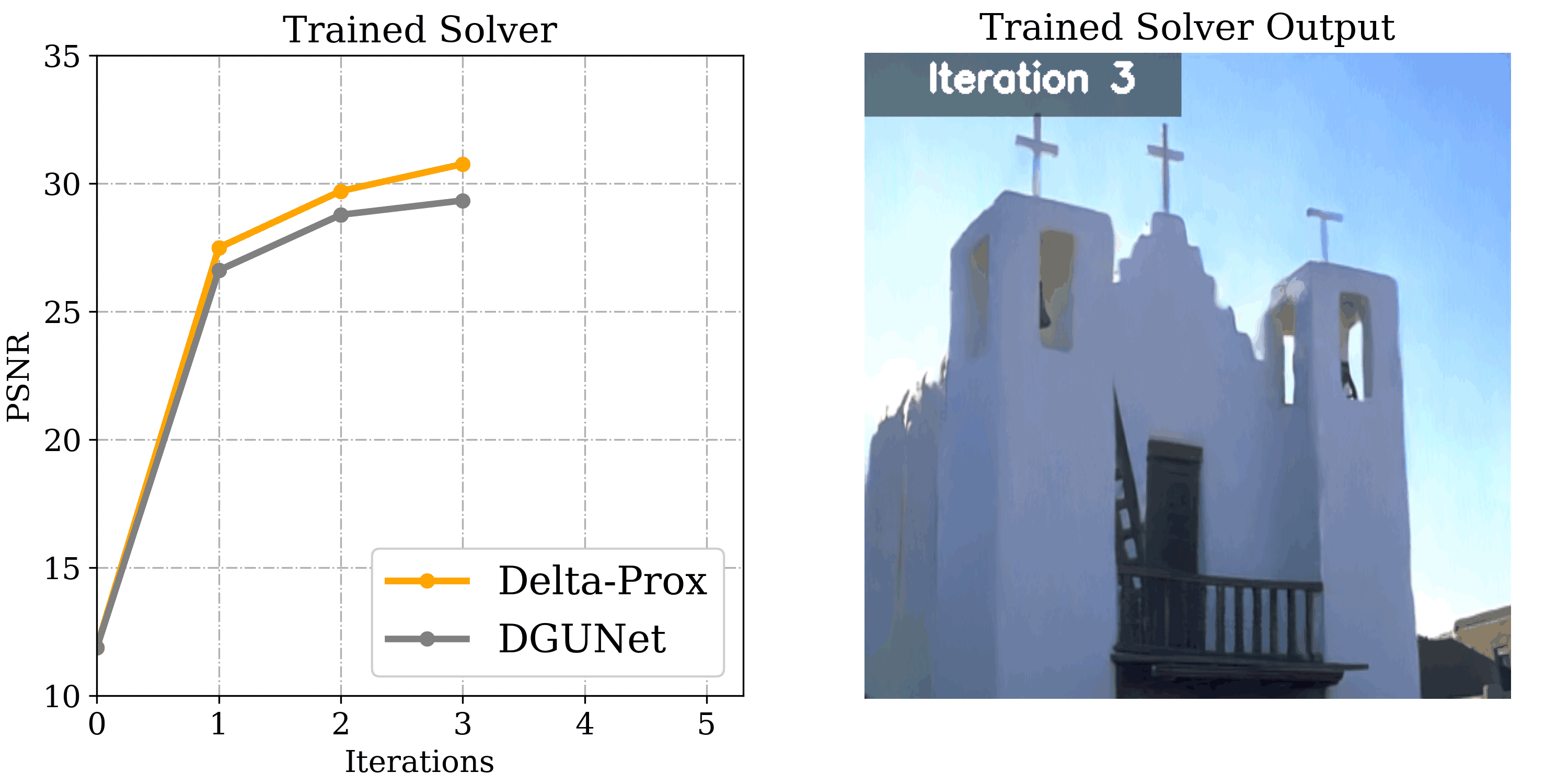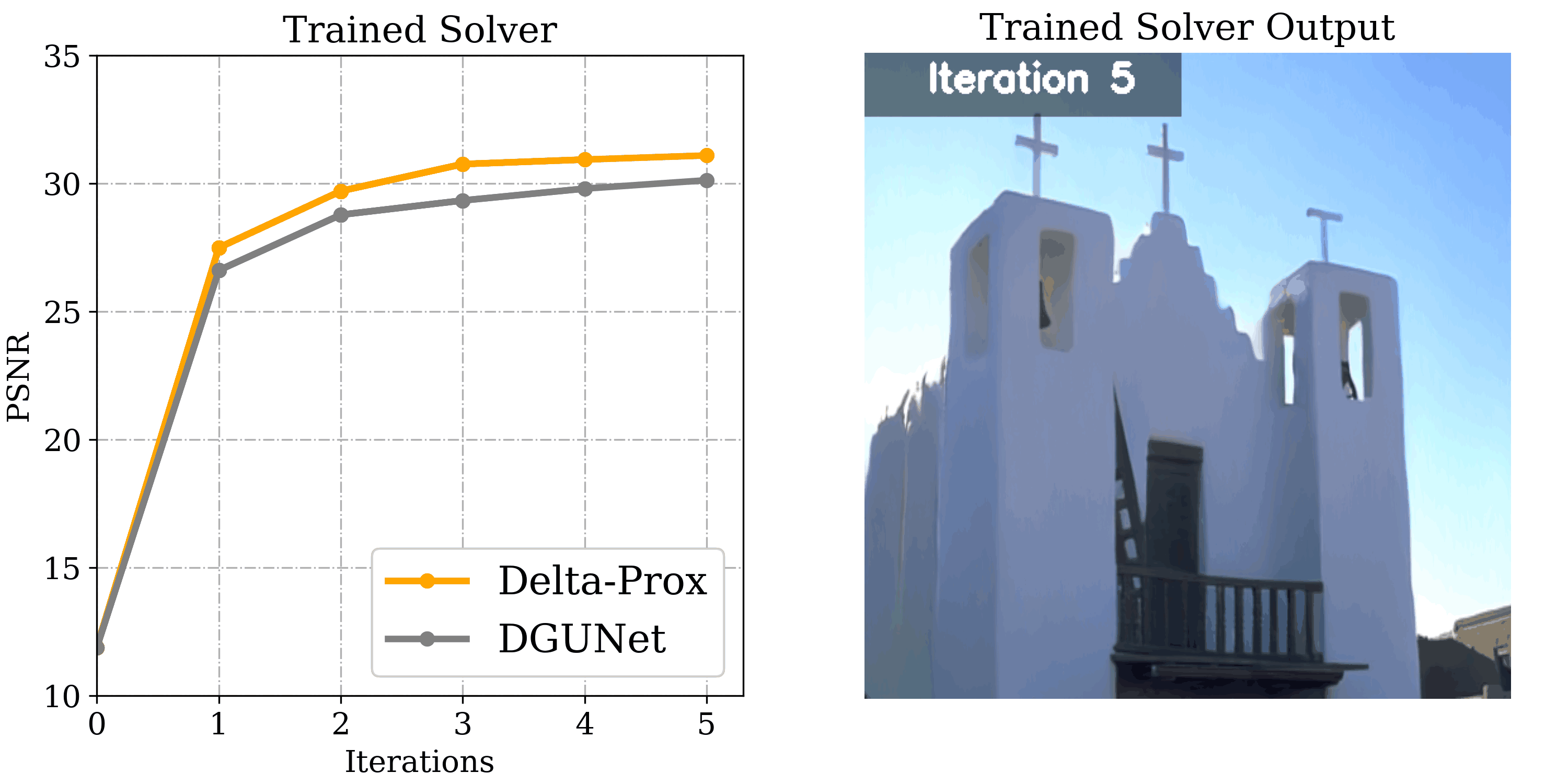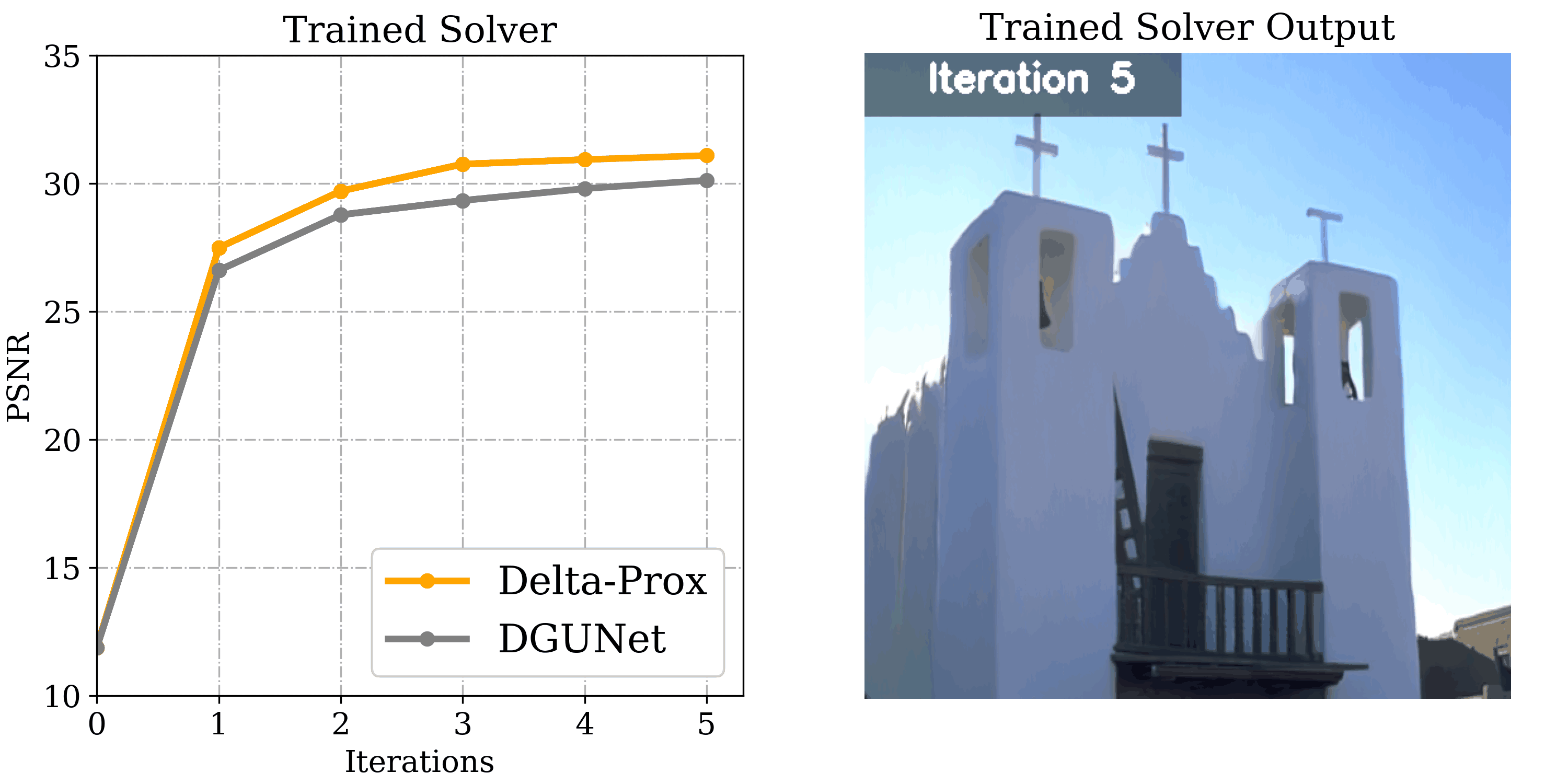
Image Deraining
Departing from image restoration problems with structured forward models, ∇-Prox also supports tackling problems where the forward model is unknown and learned alongside the optimization, such as image deraining. Being able to compile differentiable solvers, ∇-Prox facilitates learnable forward operators to encode the degradation forward process.
x = Variable() psf = build_doe_model().psf data_term = sum_squares(LearnedLinOp(x, psf) - y) reg_term = unrolled_prior(x, 'ffdnet', trainable=True) objective = data_term + reg_term solver = compile(objective, method='admm').solve() init = Initializer() out = solver.solve(x0=init(b))
Integrated Energy System Planning
Besides the imaging applications, ∇-Prox can also be effective in a seemingly orthogonal application domain, the integrated energy system planning domain — a field that describes the energy system in mathematical models typically formulated as optimization problems. Solving energy planning tasks is essential in the transition to climate neutrality of regional and global energy systems, providing decision support to policymakers by gaining insights into complex interactions and dynamics of increasingly integrated energy systems.
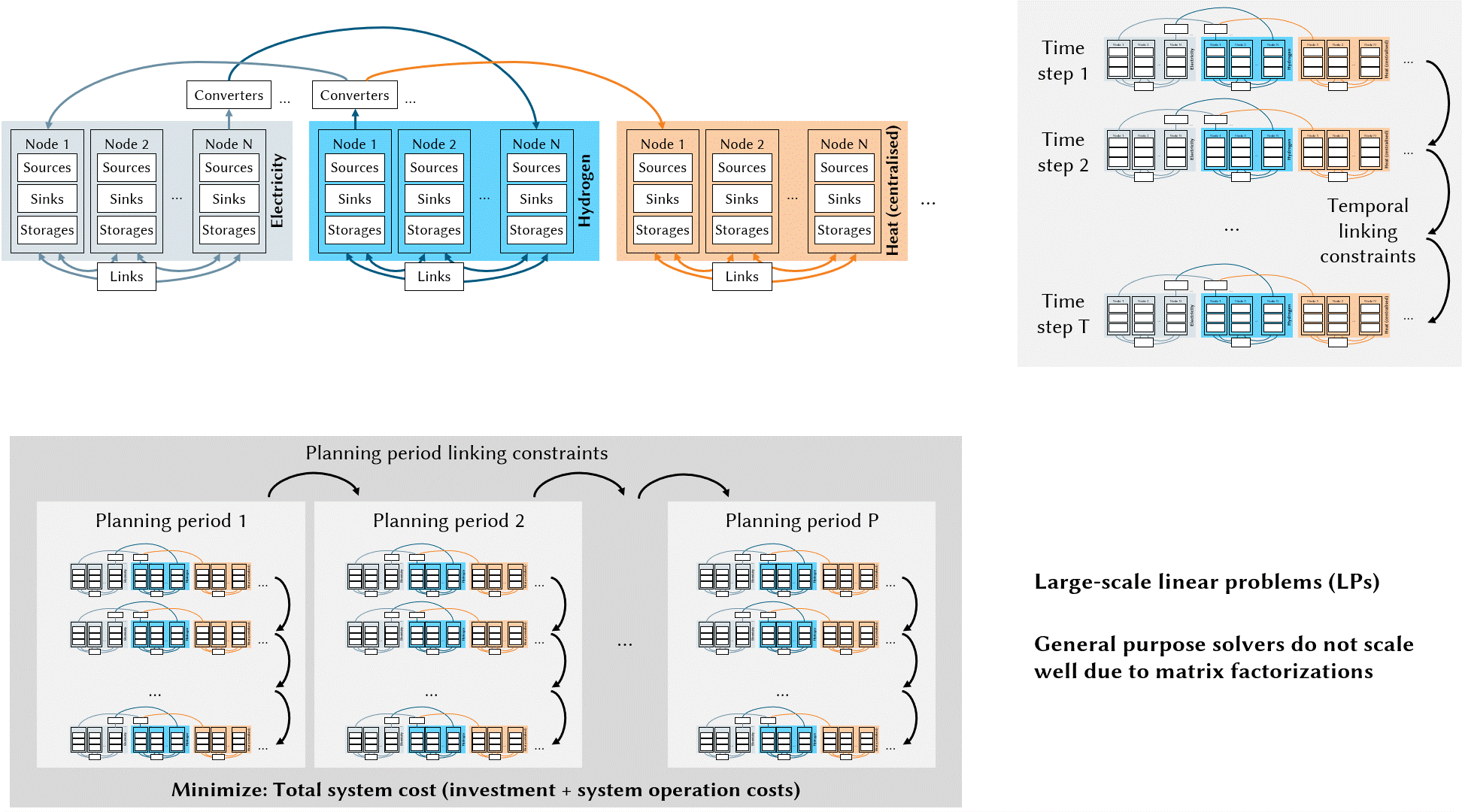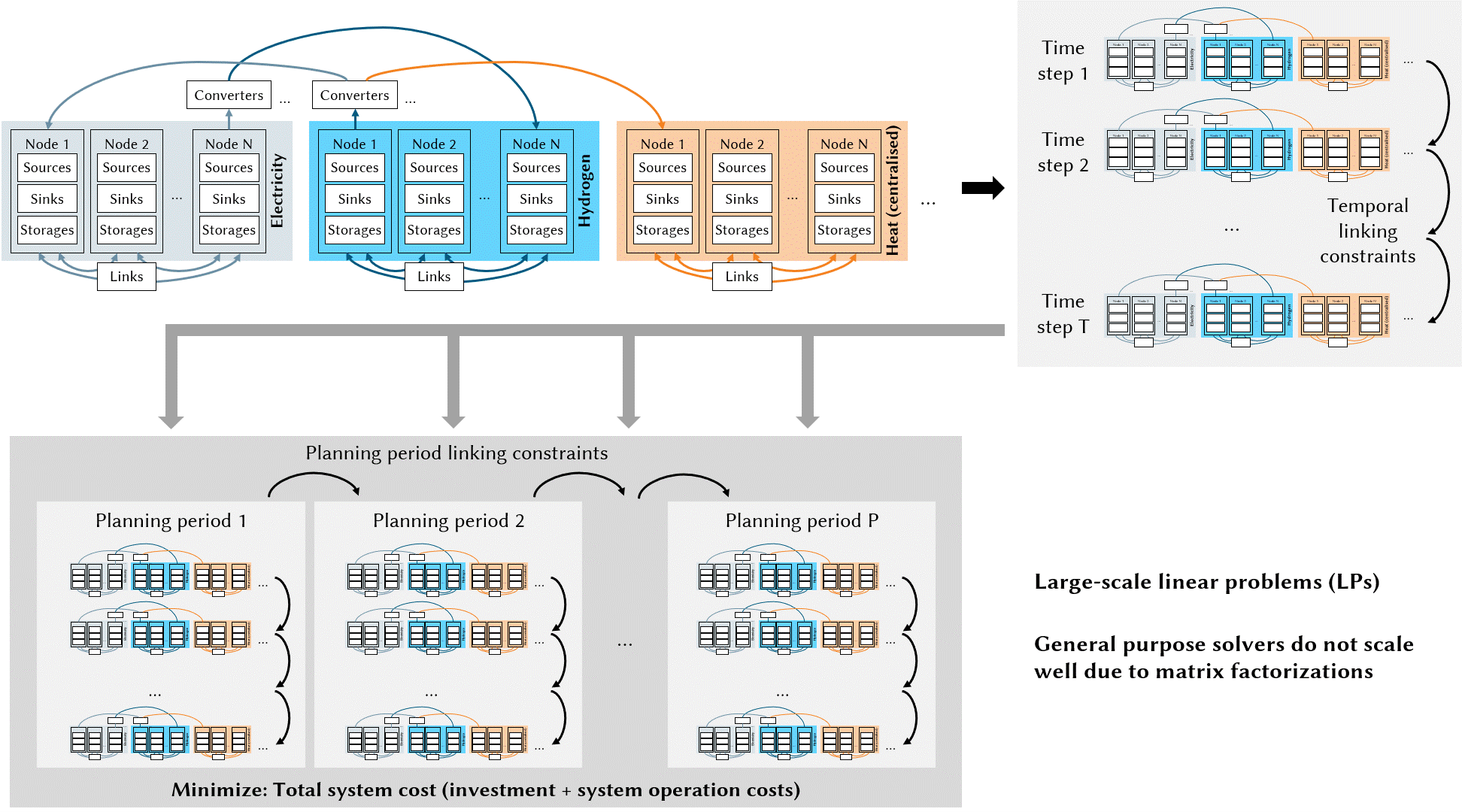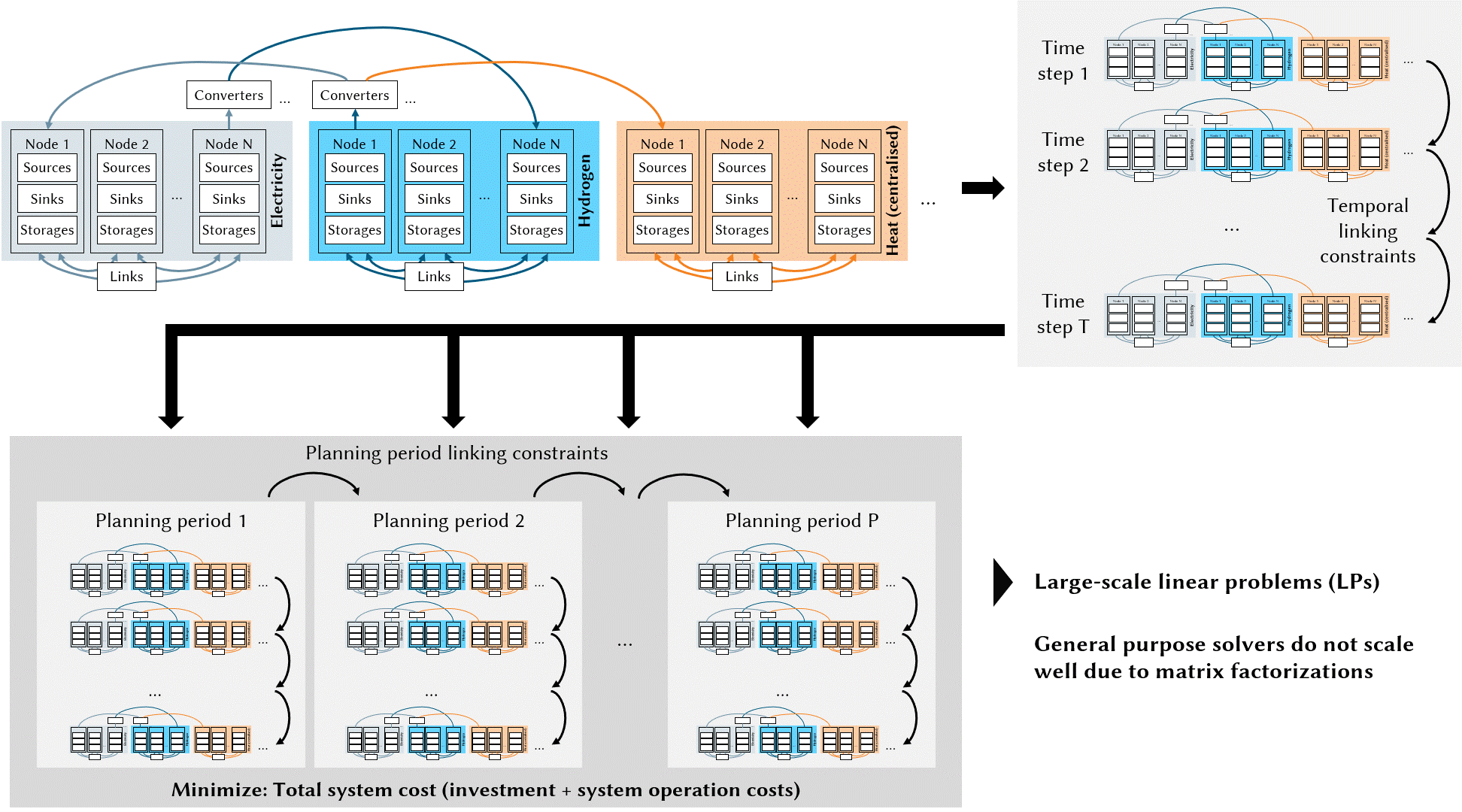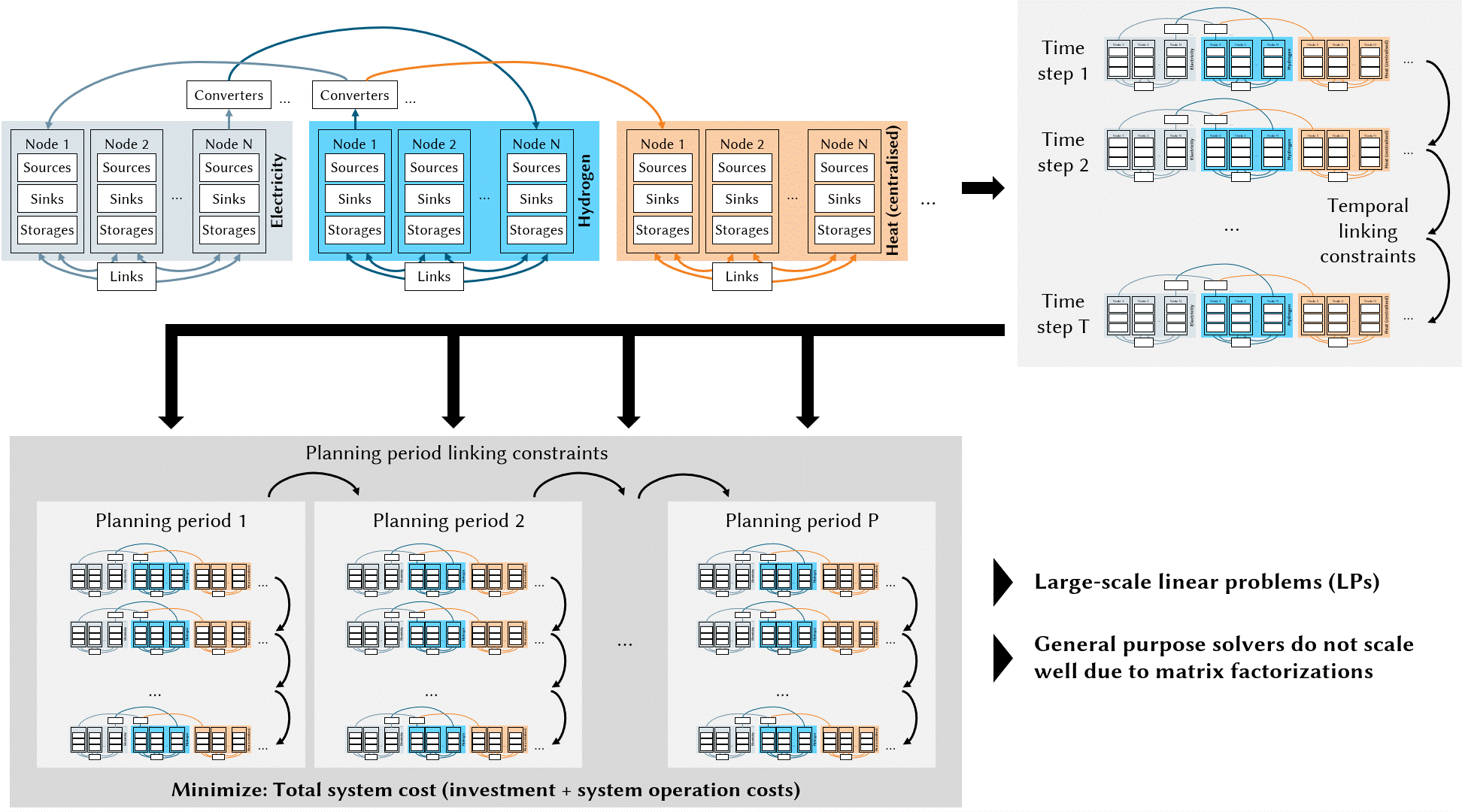
The planning problems corresponding to large-scale energy systems (up to 100 million decision variables) are typically formulated as continuous linear programming. Implementing linear programming in ∇-Prox can be prototyped as follows.
x = Variable() prob = Problem(c @ x, [A_ub @ x <= b_ub, A_eq @ x == b_eq]) out = prob.solve(method='admm', adapt_params=True)
Related Publications
[1] Felix Heide, Steven Diamond, Matthias Nießner, Jonathan Ragan-Kelley, Wolfgang Heidrich, and Gordon Wetzstein. 2016. Proximal: Efficient image optimization using proximal algorithms. ACM Transactions on Graphics (TOG) 35, 4 (2016), 1–15.
[2] Felix Heide, Markus Steinberger, Yun-Ta Tsai, Mushfiqur Rouf, Dawid Pająk, Dikpal Reddy, Orazio Gallo, Jing Liu, Wolfgang Heidrich, Karen Egiazarian, et al. 2014. Flexisp: A flexible camera image processing framework. ACM Transactions on Graphics (TOG) 33, 6 (2014), 1–13.
[3] Kaixuan Wei, Angelica Aviles-Rivero, Jingwei Liang, Ying Fu, Hua Huang, and Carola-Bibiane Schönlieb. 2022a. TFPNP: Tuning-free plug-and-play proximal algorithms with applications to inverse imaging problems. Journal of Machine Learning Research (JMLR) 23, 16 (2022), 1–48.
