Diffusion-SDF: Conditional Generative Modeling of
Signed Distance Functions
ICCV 2023
Probabilistic diffusion models have achieved state-of-the-art results for image synthesis, inpainting, and text-to-image tasks. However, they are still in the early stages of generating complex 3D shapes.
This work proposes Diffusion-SDF, a generative model for shape completion, single-view reconstruction, and reconstruction of real-scanned point clouds. We use neural signed distance functions (SDFs) as our 3D representation to parameterize the geometry of various signals (e.g., point clouds, 2D images) through neural networks. Neural SDFs are implicit functions and diffusing them amounts to learning the reversal of their neural network weights, which we solve using a custom modulation module.
Extensive experiments show that our method is capable of both realistic unconditional generation and conditional generation from partial inputs. This work expands the domain of diffusion models from learning 2D, explicit representations, to 3D, implicit representations.
Diffusion-SDF: Conditional Generative Modeling of
Signed Distance Functions
Gene Chou, Yuval Bahat, Felix Heide
ICCV 2023
Modulating SDFs
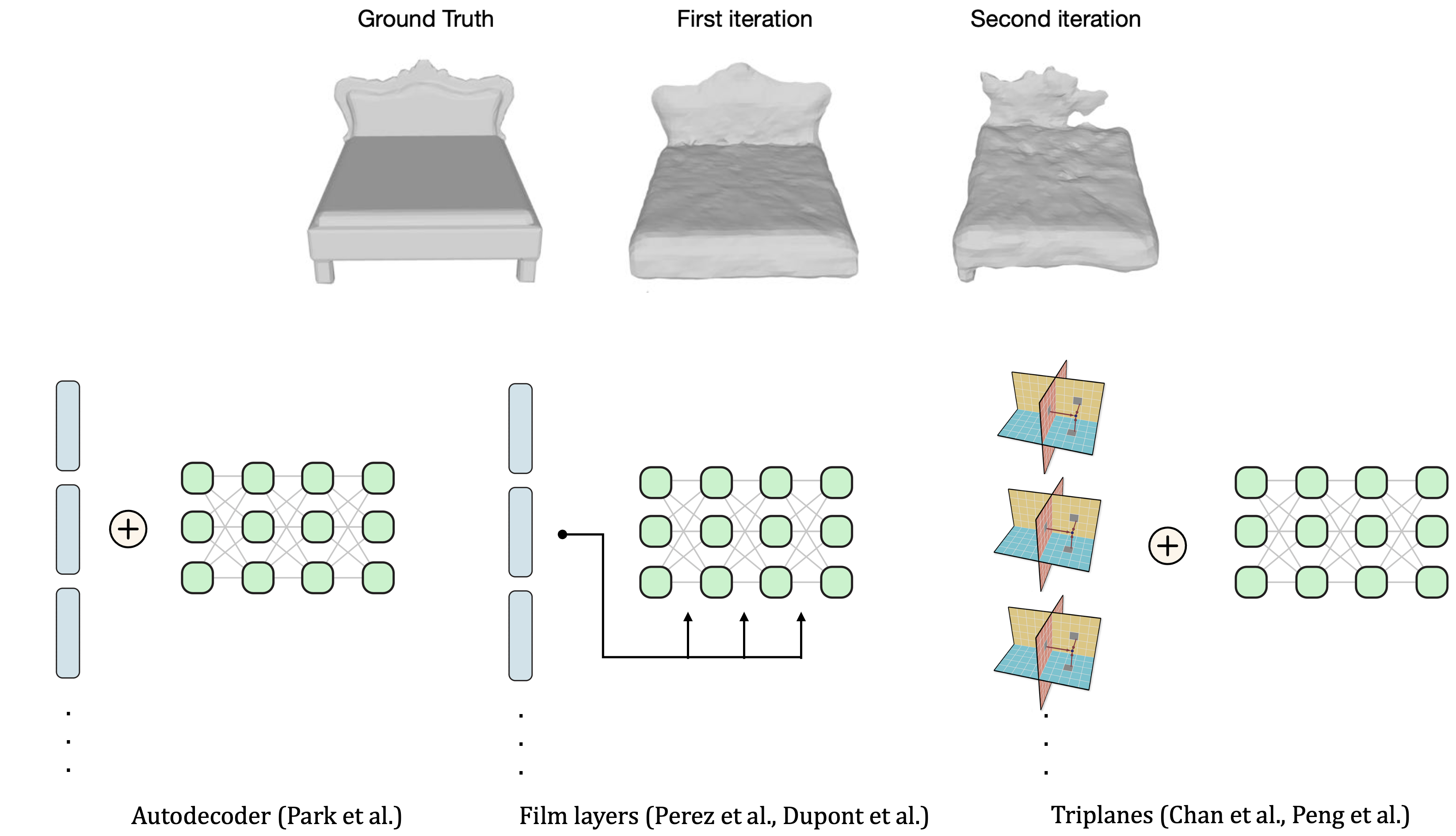
Directly diffusing thousands of SDFs, where one SDF represents one object, has two main problems. First, to obtain a network for each object, we need to train it for 1-2 hours, so training thousands or (in the future) millions of 3d objects separately would be impractical. Second, when we applied diffusion to one object, which is essentially memorizing the weights of one neural network, the noise in the slight difference in memorized vs ground-truth weights led to noisy geometric outputs (see top figure on the right).
Thus, we group all SDFs using a shared network with smaller individual representations. This means we can train all SDFs using one model to save time and we can also make the model more robust to noise. We experimented with a few methods: autodecoders, Film layers, meta-learning, and triplanes. The final option (triplanes) turned out to retain the most spatial information and is still memory-efficient.
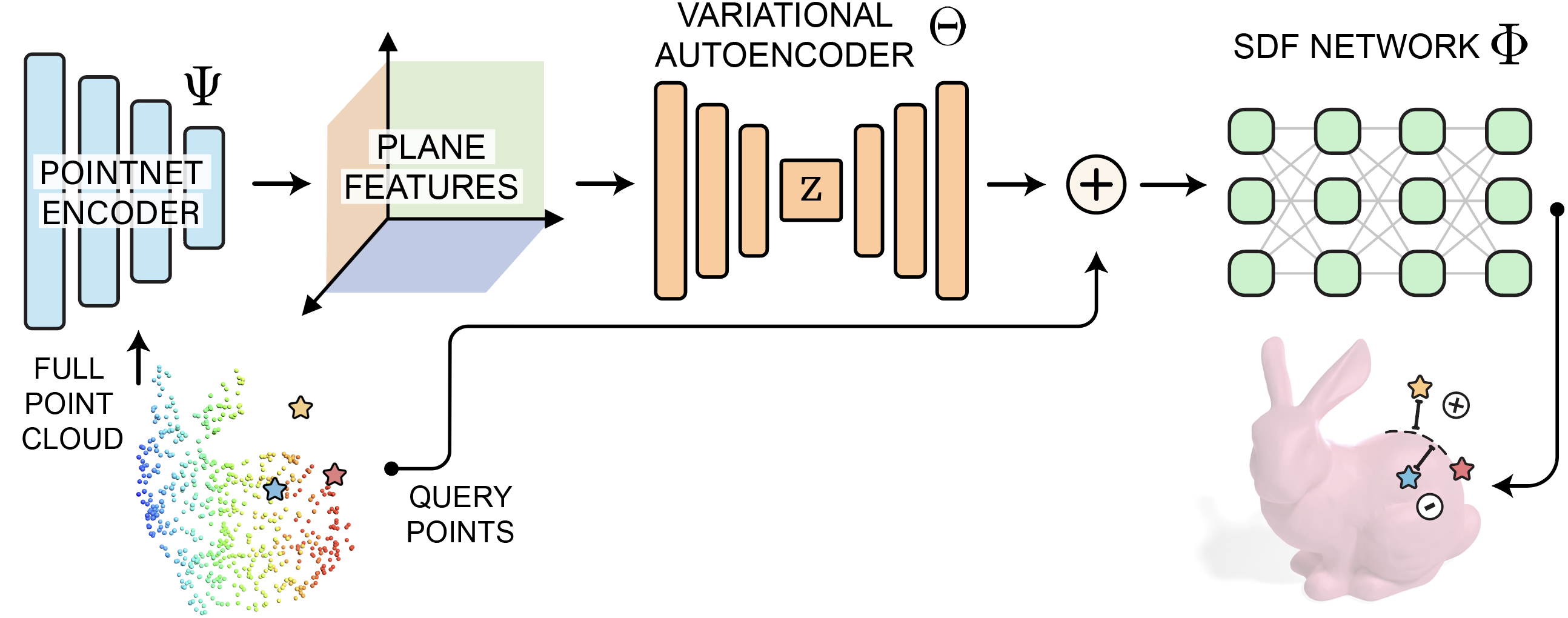
Compressing Triplane Features
We further map the triplanes to 1D latent vectors by jointly training a conditional SDF network and a VAE. Three objectives: 1. The 1D latents are memory-efficient. 2. Makes diffusion training more robust because we can use a KL divergence loss term to make the distribution easier to learn from. 3. Since there are variations in the output of the VAE, the SDF network becomes more robust to noise. Finally, the outputs of the diffusion model are mapped back to an SDF.
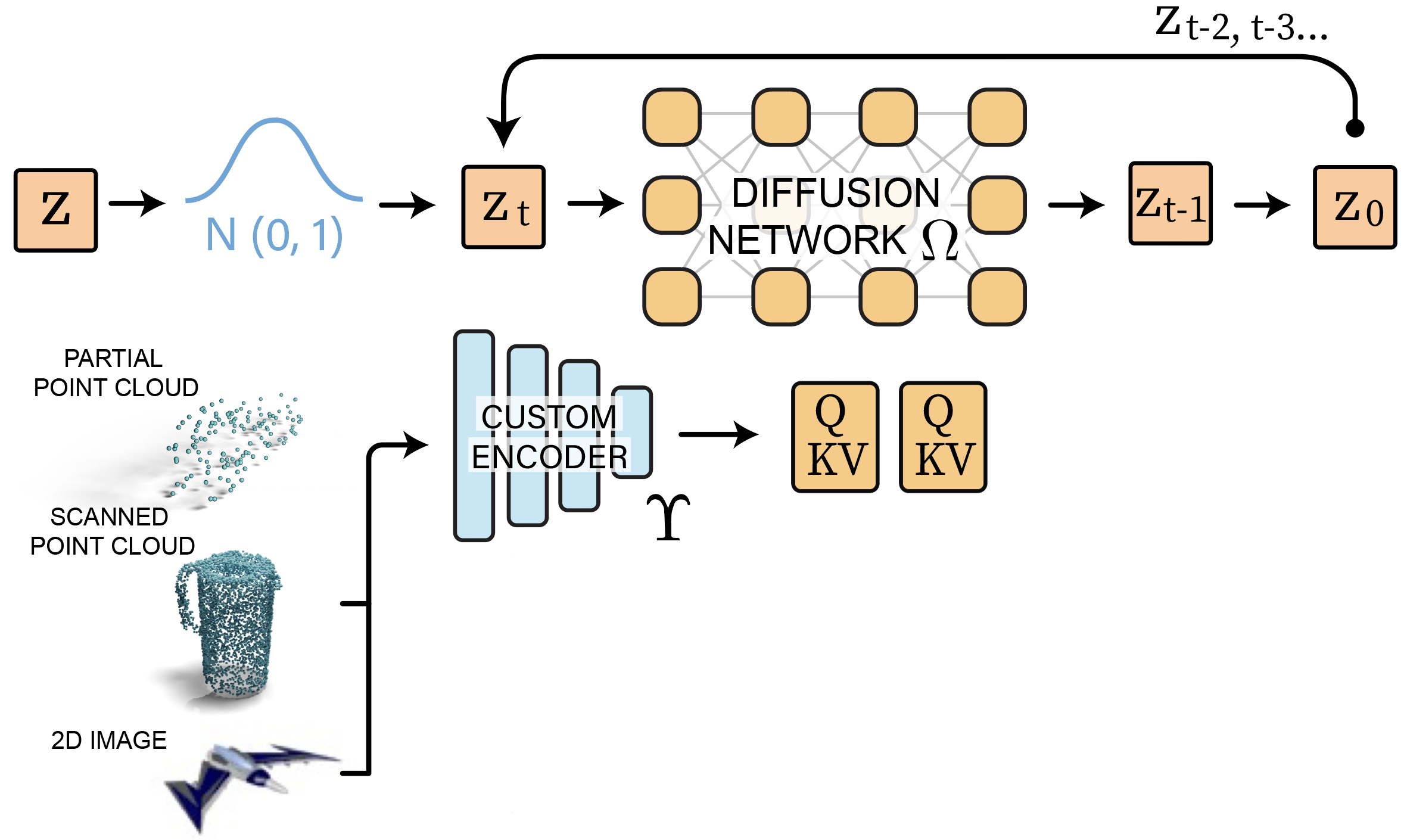
Diffusing Modulation Vectors
Next, we use our sampled latent vectors ${z}$ from the previous step as sample space for the proposed diffusion probabilistic model. In every iteration, Gaussian noise is added to the latent vectors at random timesteps, and the model learns to denoise the vectors. The denoised modulation vector $z’$ is passed back to our SDF-VAE model to obtain a final generated SDF.
Furthermore, given some condition $y$, we can train a custom encoder $\Upsilon$ to extract shape features and leverage cross-attention to guide multi-modal generations.
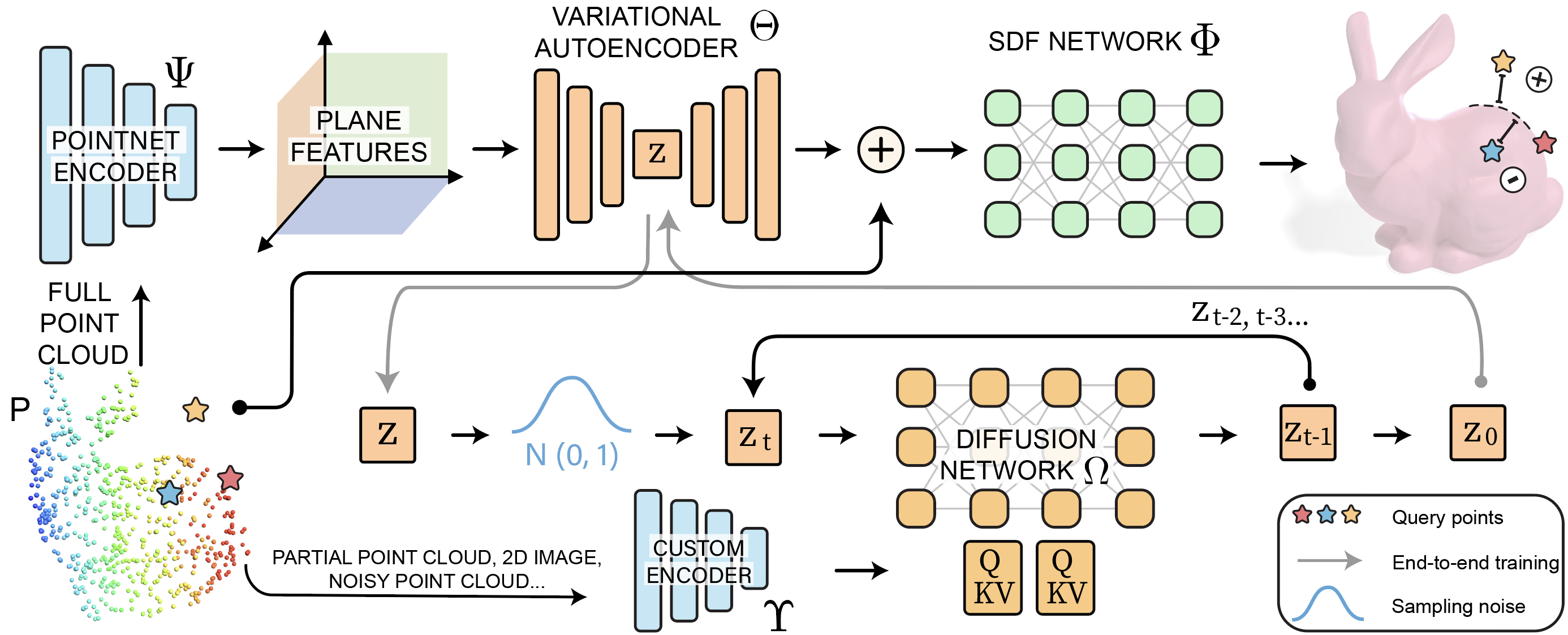
Tuning End-to-End
Our joint SDF-VAE model and diffusion model can be trained end-to-end. As shown by the gray arrow, the output of the VAE can directly be used as input to the diffusion model, whose output can then be fed into the VAE decoder for calculating its SDF loss. In practice, we found that optimizing end-to-end from scratch took too long. Instead, after the two modules are trained separately, we fine-tune them end-to-end to improve generation diversity and quality.
Unconditional Generations

Different Modalities

Generations Guided by Partial Point Clouds

Interpolation

