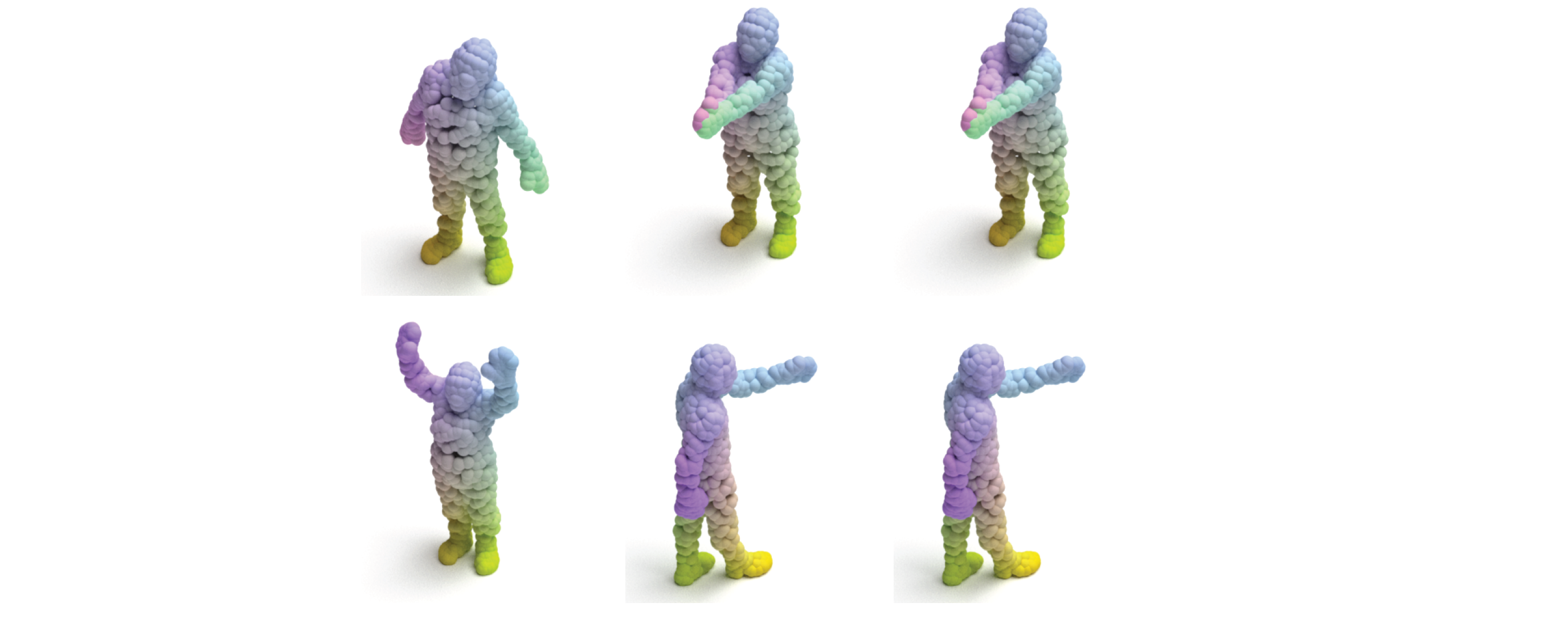Kissing to Find a Match:
Efficient Low-Rank Permutation Representation

Example Application - Non-rigid Shape Matching:
Incorporating our permutation matrix representation approach into the state-of-the-art shape-matching approach by Marin et al. [1]. Color-coding in this example signifies point correspondence between reference (left column) and input shapes, obtained using either our proposed stochastic (right) or full matrix (middle) training schemes. Please refer to the paper for details.

Permutation matrices play a key role in matching and assignment problems across the fields, especially in computer vision and robotics. However, memory for explicitly representing permutation matrices grows quadratically with the size of the problem, prohibiting large problem instances. In this work, we propose to tackle the curse of dimensionality of large permutation matrices by approximating them using low-rank matrix factorization, followed by a nonlinearity. To this end, we rely on the Kissing number theory to infer the minimal rank required for representing a permutation matrix of a given size, which is significantly smaller than the problem size. This leads to a drastic reduction in computation and memory costs, e.g., up to $3$ orders of magnitude less memory for a problem of size $n=20000$, represented using $8.4\times10^5$ elements in two small matrices instead of using a single huge matrix with $4\times 10^8$ elements. The proposed representation allows for accurate representations of large permutation matrices, which in turn enables handling large problems that would have been infeasible otherwise. We demonstrate the applicability and merits of the proposed approach through a series of experiments on a range of problems that involve predicting permutation matrices, from linear and quadratic assignment to shape matching.

Geometric intuition behind our approach on a 2D unit sphere:
For well-distributed vectors $V \in \mathbb{R}^{\text{kissing}(2) \times 2}$, where the number of vectors is determined by the Kissing number ($\text{kissing}(2) = 6$), the cosine angle between different vectors $V_{i,:}$ and $V_{j,:}$, $i \neq j$, is $\langle V_{i,:}, V_{j,:}\rangle = \cos(\alpha) \leq 0.5$, while $\langle V_{i,:}, V_{i,:}\rangle = 1$ for the same vector. Thus, for any permutation $P$, the matrix-matrix product of $V$ and $(PV)^T$ merely has to be thresholded suitably to represent the permutation $P$, i.e. $P = 2\max(V(PV)^T - 0.5,0)$.

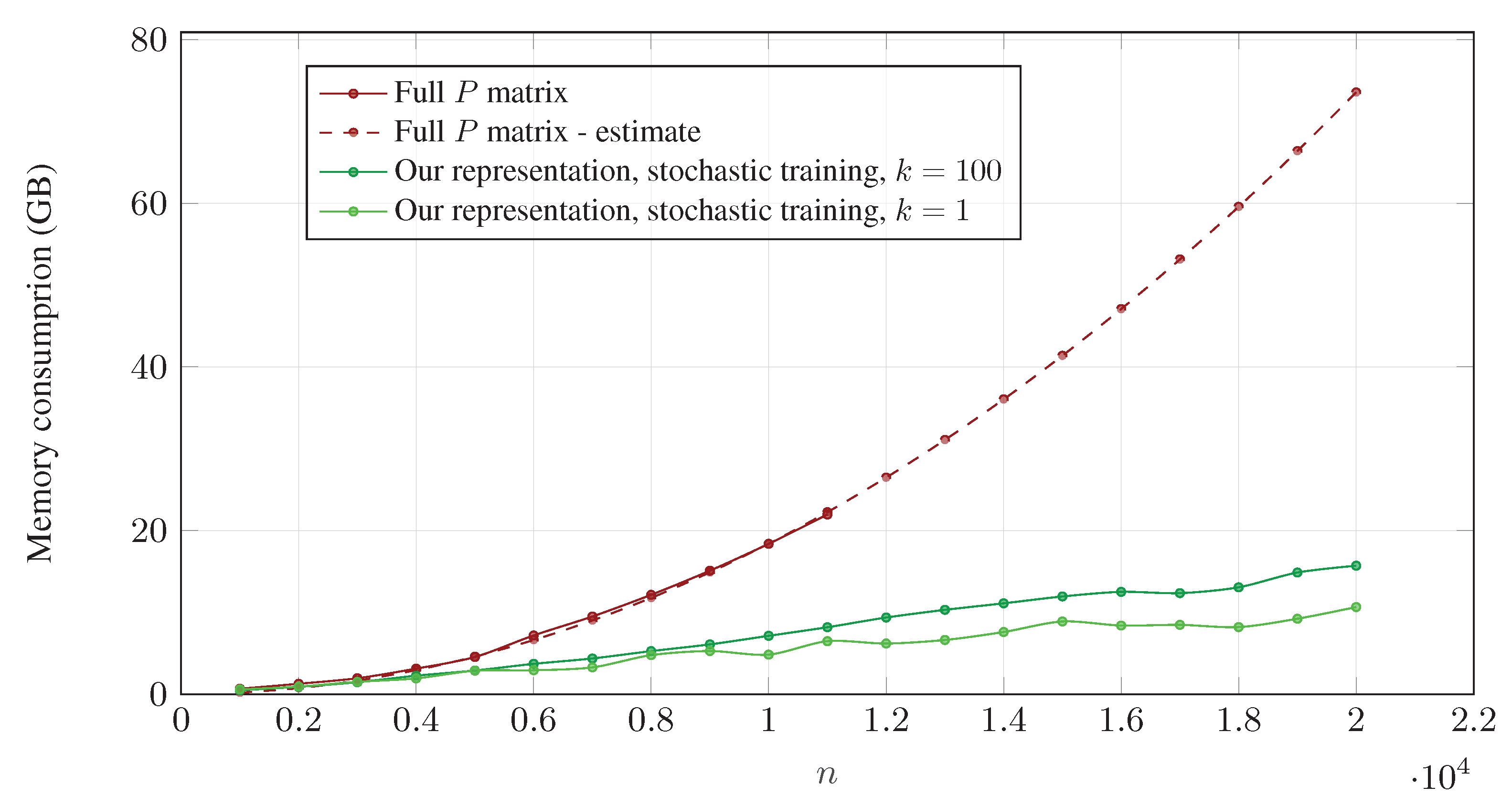
Handling Large Permutation Matrices:
Our approach enables handling large problems that would have been infeasible otherwise, for instance in shape matching problems.
The dashed red curve on the right corresponds to the estimated memory that would have been required to accommodate full permutation matrices, as a function of problem size $n$. While our approach can accurately handle large problems with as much as $n=20,000$ vertices (green curves), running the equivalent experiments without it (red curves) would require prohibitively large amounts of memory ($\sim73.6~\text{GB}$, vs. $10.7~\text{GB}$ using $k=1$). For estimating memory values (dashed curve) we assume memory usage follows a $c\cdot n^2$ curve, and estimate the value for $c$ based on the full matrix experiments (solid red) we conducted for $n\leq11,000$. Please refer to the paper for details on the stochastic training scheme and $k$.