GenSDF: Two-Stage Learning of Generalizable
Signed Distance Functions
NeurIPS 2022 (Featured)
Neural signed distance functions (SDFs) implicitly model the distance from a queried location to the nearest point on a shape’s surface — negative inside the shape, positive outside, zero at the surface. Existing methods are capable of approximating diverse synthetic geometry and varying levels of detail. However, most successful methods are fully supervised–they require access to ground truth signed distance values to fit an object. As raw point clouds lack these values, a fully-supervised approach cannot learn from in-the-wild data.
In this work, we introduce a two-stage semi-supervised meta-learning approach that transfers shape priors from labeled to unlabeled data to reconstruct unseen object categories. The first stage uses an episodic training scheme to simulate training on unlabeled data and meta-learns initial shape priors. The second stage then introduces unlabeled data with disjoint classes in a semi-supervised scheme to diversify these priors and achieve generalization. We assess our method on both synthetic data and real collected point clouds. Experimental results and analysis validate that our approach outperforms existing neural SDF methods and is capable of robust zero-shot inference on 100+ unseen classes.
Convolutional OccNets
GenSDF (ours)
(In Browser: Click and Drag to Rotate, Scroll to Zoom)
GenSDF: Two-Stage Learning of Generalizable
Signed Distance Functions
Gene Chou, Ilya Chugunov, Felix Heide
NeurIPS 2022 (Featured)
Two stage meta-learning semi-supervised approach
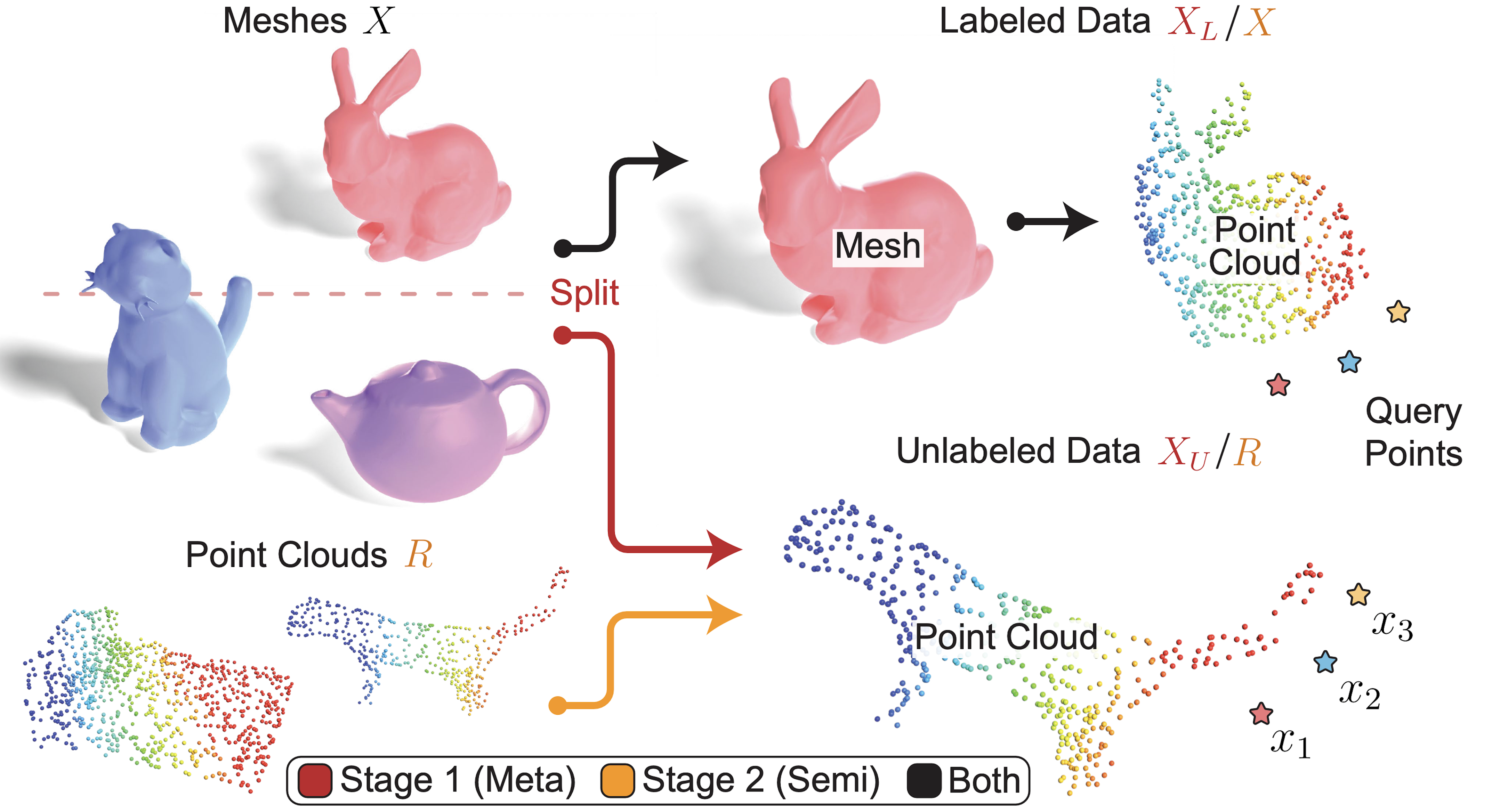
We want to train on labeled and unlabeled data simultaneously, so we mimic this goal in a meta-learning approach as we learn shape priors from $X$. Every few epochs, we split $X$ into two subsets $X_L$ and $X_U$ with disjoint categories. We train $X_L$ with a supervised loss, similar to typical supervised approaches on labeled data. We take away ground-truth signed distance values from $X_U$ making it “pseudo-unlabeled”, and train it with our self-supervised loss. Compared to directly training on labeled and unlabeled data, this meta-learning process provides flexibility as we can tune the split frequency and ratio of labeled and “pseudo-unlabeled” data. The model repeatedly sees the same point clouds with and without labels, so shape features generated during labeled splits are shared with “pseudo-unlabeled” splits.
In our second stage, we train our conditional SDF from the meta-learning stage on both labeled and unlabeled data in a semi-supervised fashion. As a result of the learned priors, training remains robust even with large amounts of unlabeled data.
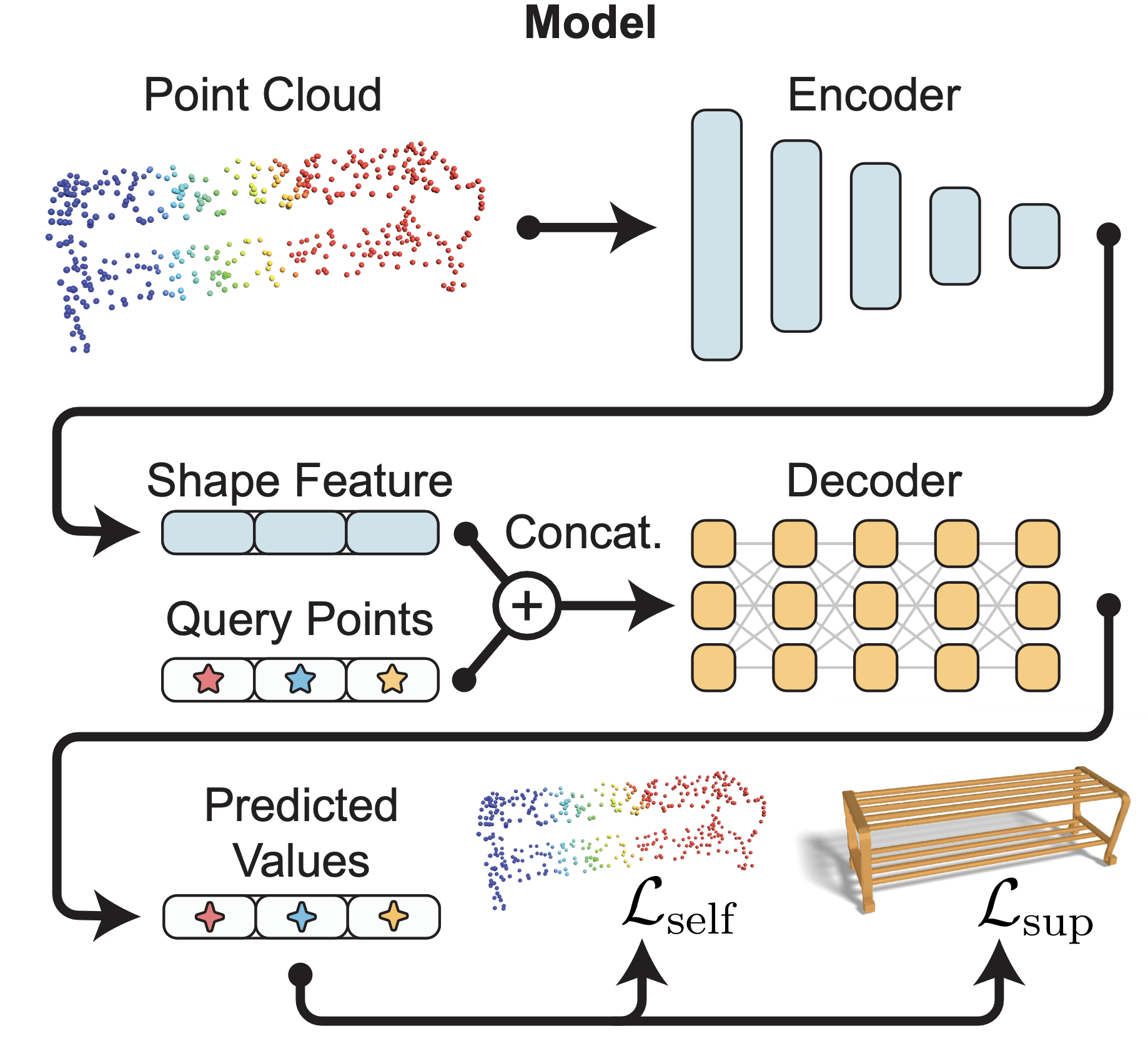
Self-supervised loss formulation
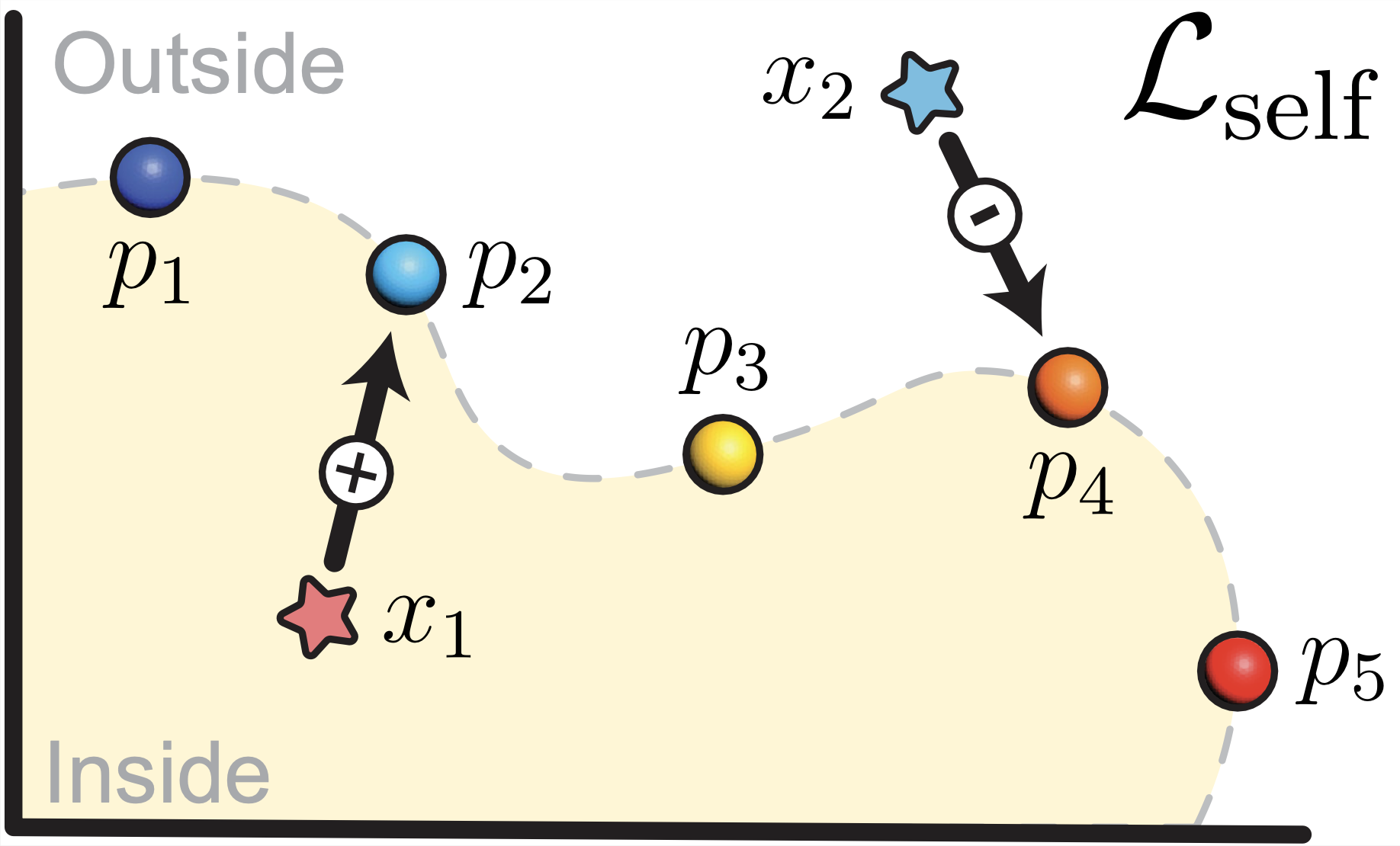
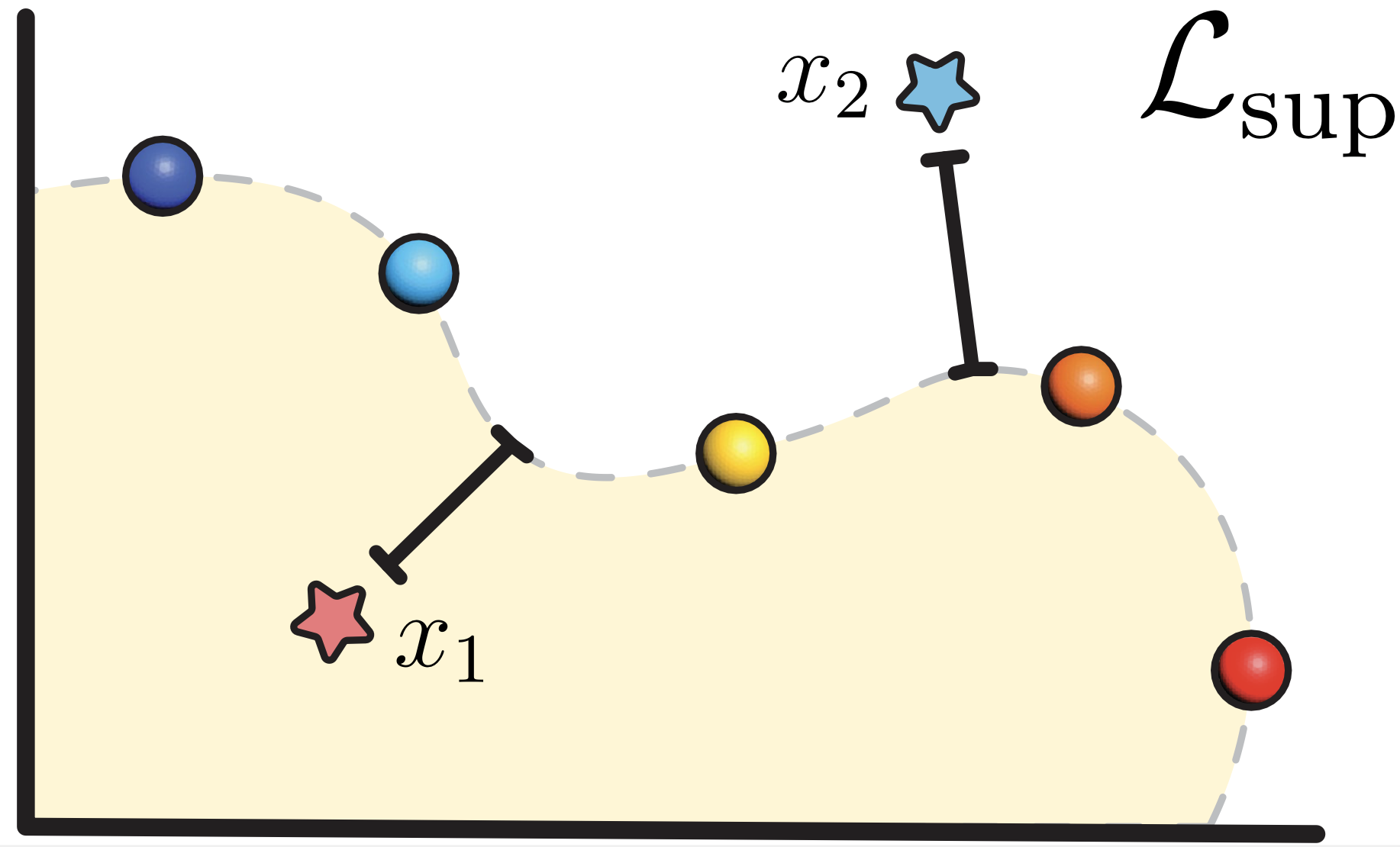
Crucial to the success of our method is our self-supervised loss for training unlabeled data. For each query point $x \in \mathbb{R}^{3}$, we use its closest point $t \in P$ (where $P$ is the full point cloud) to approximate its projection to the surface.
Our insight is that we want to predict $\hat{t}$ to approximate $t$ on the point cloud by using the predicted signed distance value and our training objective is to minimize the distance between the two. Different from existing work, our formulation has an explicit penalty for incorrect sign predictions. We denote our approach self-supervised because the predictions of the signs are used as labels.
We have
\begin{equation}
\mathcal{L}_{\mathrm{self}} = \frac{1}{K} \sum_{k \in K} \| \hat{t}_k – t_k \|_2^2,
\label{selfeq}
\end{equation}
\begin{equation}
\hat{t} =\begin{cases}
x – \frac{x-t}{\|x-t\|} \ \Phi(x) & \text { if } \Phi(x) \ge 0, \\[2em]
x + \frac{x-t}{\|x-t\|} \ \Phi(x) & \text { if } \Phi(x) < 0 .
\end{cases}
\label{t_eq}
\end{equation}
$\mathcal{L}_{\mathrm{self}}$ is our self-supervised loss and $\Phi(\cdot) $ is our trained neural network.
Evaluation of real point cloudsWe test our model on the YCB dataset, which is a real-world point cloud dataset acquired from multi-view RGBD captures. The fused multi-view point clouds in this dataset resemble input measurements for a robotic part-picking or manipulation task. We demonstrate robust mesh reconstructions of the measured data, e.g., recovering the “handle” of a pitcher, which may serve as input to complex robotic grasping tasks. YCB is a different domain from the synthetic training dataset, but our proposed method is able to approximate the 3D shape with detail, illustrating its ability of handling in-the-wild and out-of-distribution data. (In Browser: Click and Drag to Rotate, Scroll to Zoom) |
Convolutional OccNets
|
GenSDF (ours)
|
Ground truth
|
Reconstructing the Acronym dataset

(Check out our main paper and supplement for more visualizations)
Reconstructing the YCB dataset



